
【题目】2016年1月6日北京时间上午11时30分,朝鲜中央电视台宣布“成功进行了氢弹试验”,再次震动世界,此事件也引起了我国公民热议,其中丹东市(丹东市和朝鲜隔江)某![]() 聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:
聊天群有300名网友,乌鲁木齐市某微信群有200名网友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名网友,先分别统计了他们在某时段发表的信息条数,再将两地网友发表的信息条数分成5组:![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.
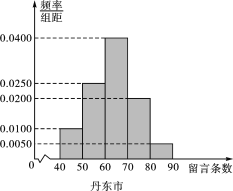
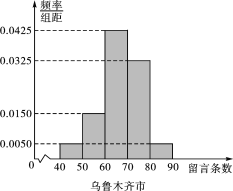
(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数不足50条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列![]() 的列联表:
的列联表:
强烈关注 | 非强烈关注 | 合计 | |
丹东市 | |||
乌鲁木齐市 | |||
合计 |
②判断是否有![]() 的把握认为“强烈关注”与网友所在的地区有关?
的把握认为“强烈关注”与网友所在的地区有关?
附:临界值表及参考公式:
![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)64;(2)![]() ;(3)①列联表见解析;②没有.
;(3)①列联表见解析;②没有.
【解析】
(1)根据频率分布直方图的平均数的计算公式得到结果;(2)根据频率分布直方图得到丹东市满足条件的人数6人,乌鲁木齐2人,随机抽取2人有28种方法,符合题目条件的有13人,根据古典概型的计算公式得到结果;(3)①根据频率分布直方图得到相应的列联表;②由公式得到卡方值,进而得到判断.
(1)45×0.01×10+55×0.025×10+65×0.04×10+75×0.02×10+85×0.005×10=63.5≈64.
所以丹东市网友的平均留言条数是64条.
(2)留言条数不足50条的网友中,丹东市网友有0.01×10×100×![]() =6(人),乌鲁木齐市网友有0.005×10×100×
=6(人),乌鲁木齐市网友有0.005×10×100×![]() =2(人),
=2(人),
从中随机抽取2人共有![]() 种可能结果,其中至少有一名乌鲁木齐市网友的结果共有CC+ C=12+1=13种情况,
种可能结果,其中至少有一名乌鲁木齐市网友的结果共有CC+ C=12+1=13种情况,
所以至少抽到一名乌鲁木齐市网友的概率为 P=![]() .
.
(3)①列联表如下:
强烈关注 | 非强烈关注 | 合计 | |
丹东市 | 15 | 45 | 60 |
乌鲁木齐市 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
②K2的观测值k=![]() =
=![]() ≈1.79.
≈1.79.
因为1.79<2.706,所以没有90%的把握认为“强烈关注”与网友所在的地区有关.


科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
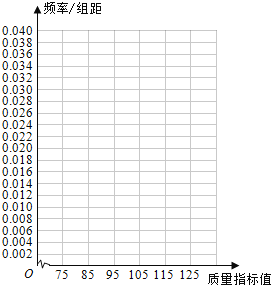
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市在2018年元旦举办了一次抽奖活动,抽奖箱里放有2个红球,1个黄球和1个蓝球(这些小球除颜色外大小形状完全相同),从中随机一次性取2个小球,每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下:
①凡购物满100(含100)元者,凭购物打印凭条可获得一次抽奖机会;
②凡购物满188(含188)元者,凭购物打印凭条可获得两次抽奖机会;
③若取得的2个小球都是红球,则该顾客中得一等奖,奖金是一个10元的红包;
④若取得的2个小球都不是红球,则该顾客中得二等奖,奖金是一个5元的红包;
⑤若取得的2个小球只有1个红球,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据(单位:元),绘制得到如图所示的茎叶图.

(1)求这20位顾客中获得抽奖机会的人数与抽奖总次数(假定每位获得抽奖机会的顾客都会去抽奖);
(2)求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数(结果精确到整数部分);
(3)分别求在一次抽奖中获得红包奖金10元,5元,2元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.已知函数
的不动点.已知函数![]()
![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求
恒有两个相异的不动点,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的两个不动点为
的两个不动点为![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).
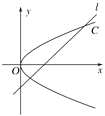
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)当p=1时,若抛物线C上存在关于直线l对称的相异两点P和Q.求线段PQ的中点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某初级中学共有学生2000名,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
求x的值;
现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
已知y![]() 245,z
245,z![]() 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com