
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。
(1)求恰有2门选修课这3个学生都没有选择的概率;
(2)设随机变量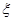 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求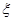 的分布列及期望,方差.
的分布列及期望,方差.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字 ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取 次,每次抽取
次,每次抽取 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为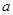 ,
,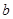 ,
,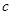 .
.
(Ⅰ)求“抽取的卡片上的数字满足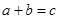 ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字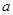 ,
,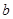 ,
,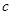 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“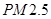 ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“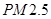 ” ” 小时平均浓度( 小时平均浓度(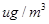 ) ) |  |  |  |  |  |  |  |  |  |  |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘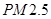 ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
做抛掷两颗骰子的试验:用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第二颗骰子出现的点数,(1)写出试验的基本事件;(2)求事件“出现点数之和大于8”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•天津)一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4; 白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率.
(2)再取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为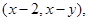 记
记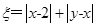 .
.
(1)求随机变量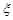 的最大值,并求事件“
的最大值,并求事件“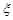 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量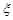 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数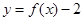 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com