已知等差数列{an}的首项a1＞0，公差d＞0，前n项和为Sn，且m＋n＝2p(m、n、p∈N*)，求证：Sn＋Sm≥2Sp.
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案科目：高中数学 来源： 题型：
设A、B分别为椭圆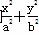
＝1(a>b>0)的左、右顶点，椭圆长半轴的长等于焦距，且直线x＝4是它的右准线．
(1) 求椭圆的方程；
(2) 设P为椭圆右准线上不同于点(4，0)的任意一点，若直线BP与椭圆相交于两点B、N，求证：∠NAP为锐角．
查看答案和解析>>
科目：高中数学 来源： 题型：
定义集合运算：A·B＝{Z|Z＝xy，x∈A，y∈B}，设集合A＝{－1，0，1}，B＝{sinα，cosα}，则集合A·B的所有元素之和为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
用反证法证明命题“a·b(a、b∈Z)是偶数，那么a、b中至少有一个是偶数．”那么反设的内容是__________________________________．
查看答案和解析>>
科目：高中数学 来源： 题型：
给出下列四个命题：
①直线垂直于一个平面内的无数条直线是这条直线与这个平面垂直的充要条件；
②过空间一定点有且只有一条直线与已知平面垂直；
③不在一个平面内的一条直线和平面内的一条直线平行是这条直线和这个平面平行的充分条件；
④一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角相等或互补．
其中真命题的为（ ）
A．①③ B．②④ C．②③ D．③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
(n∈N*)，则a3＝________，a1·a2·a3·…·a2007＝________．
＋
＋
＋…＋
(n∈N*)，则f(k＋1)－f(k)＝________.