本试题主要考查了立体几何中的线面的垂直,以及二面角的求解的综合运用。
解:(I)由三视图知PC⊥面ABCD,ABCD为正方形,且PC=2,AB=BC=1(2分)
∴VP-ABCD="1" /3 •S
ABCD×PC="1" /3 •1
2•2="2" /3 (1分)
(II)∵PC⊥面ABCD,BD?面ABCD∴PC⊥BD …(1分)而BD⊥AC,AC∩AE=A,
∴BD⊥面ACE,…(1分)而AE?面ACE∴BD⊥AE (1分)
(III)法一:连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,设θ为二面角O-AE-B的平面角.注意到B在面ACE上的射影为O
S△AOE="1/" 2 S△ACE="1" /2 ×1/ 2 ×
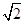
=
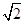
/ 4 .
S△ABE="1" /2 AB•BE=
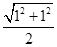
=
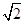
/ 2 ,(2分)∴cosθ=S△AOE /S△ABE ="1" /2
∴θ=60°∴二面角D-AE-B是120°(2分)
法二:以C为坐标原点,CD所在直线为x轴建立空间直角坐标系
则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
从而 DE =(-1,0,1), DA =(0,1,0),
BA =(1,0,0), BE =(0,-1,1)(2分)
设平面ADE和平面ABE的法向量分别为
n
1 =(x
1,y
1,z
1), n
2 =(x
2,y
2,z
2)则-x
1+z
1=0,y
1=0
x
2=0,-y
2+z
2=0令z
1=1,z
2=-1,则 n
1 =( (1,0,1), n
2 =(0,-1,-1)(2分)
设二面角D-AE-B的平面角为θ,则|cosθ|="|" n
1 • n
2 | /| n
1 | ×| n
2| = 1 /2 .
二面角D-AE-B为钝二面角.∴二面角D-AE-B的大小为2π/ 3 .

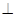 AE?试证明你的结论;
AE?试证明你的结论;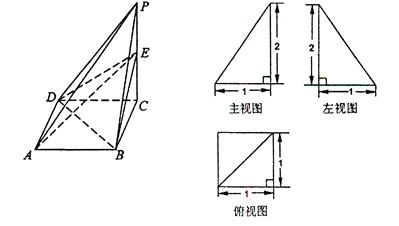
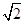 =
= 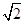 / 4 .
/ 4 .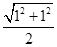 =
= 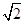 / 2 ,(2分)∴cosθ=S△AOE /S△ABE ="1" /2
/ 2 ,(2分)∴cosθ=S△AOE /S△ABE ="1" /2 
