
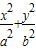 =1(a>b>0)的短轴长为4,F1F2分别是椭圆C的左,右焦点,直线y=x与椭圆C在第一象限内的交点为A,△AF1F2的面积为2
=1(a>b>0)的短轴长为4,F1F2分别是椭圆C的左,右焦点,直线y=x与椭圆C在第一象限内的交点为A,△AF1F2的面积为2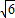 ,点P(x,y),是椭圆C上的动点w.
,点P(x,y),是椭圆C上的动点w.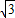 PF1+
PF1+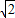 PA的最小值.
PA的最小值.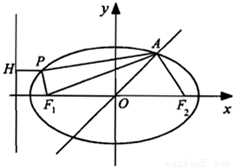
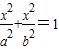 ,②结合△AF1F2的面积为2
,②结合△AF1F2的面积为2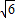 ,有cx=2
,有cx=2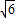 ③,由①②③得a,最后写出椭圆C的方程;
③,由①②③得a,最后写出椭圆C的方程;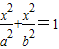 ,②
,②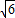 ,∴cx=2
,∴cx=2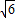 ③,
③,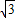 ,椭圆C的方程为:
,椭圆C的方程为: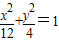 .
.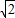 ,0),F2(2
,0),F2(2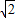 ,0),
,0),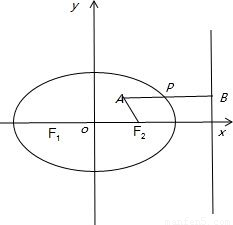
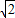 )2+y2+(x-2
)2+y2+(x-2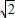 )2+y2<32
)2+y2<32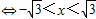 .
.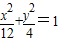 与y=x(x>0)解得A(
与y=x(x>0)解得A(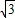 ,
,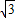 ),
),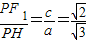 ,
,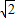 ,
,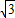 PF1+
PF1+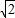 PA即为:
PA即为: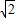 (PH+PA)
(PH+PA)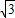 +3
+3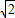 ,
,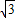 PF1+
PF1+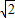 PA的最小值
PA的最小值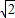 (
(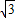 +3
+3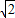 )=6+
)=6+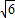 .
.

科目:高中数学 来源:2013年四川省资阳市高考数学二模试卷(文科)(解析版) 题型:解答题
 +
+ =1(a>b>0)经过(1,1)与(
=1(a>b>0)经过(1,1)与( ,
, )两点.
)两点. +
+ +
+ 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源:2012年陕西省高考数学压轴卷(解析版) 题型:选择题
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



查看答案和解析>>
科目:高中数学 来源:2012年吉林省高考数学仿真模拟试卷9(理科)(解析版) 题型:解答题
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
查看答案和解析>>
科目:高中数学 来源:2011年高考数学总复习备考综合模拟试卷(3)(解析版) 题型:解答题
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省攀枝花市高三12月月考文科数学试卷(解析版) 题型:解答题
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
(1)求椭圆方程;
(2)若直线 :
: 与
与 轴交于点T,P为
轴交于点T,P为 上异于T的任一点,直线
上异于T的任一点,直线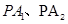 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com