
本小题满分10分)
在△ABC中,A、B为锐角,角A、B、C所对的边分别为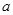 、
、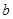 、
、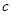 ,且
,且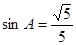 ,
,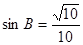 。
。
(1)求角C的值;
(2)若a-b=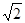 -1,求
-1,求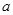 、
、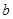 、
、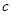 的值。
的值。
(1)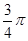 ;(2)a=
;(2)a=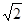 ,b=1,c=
,b=1,c=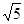 。
。
【解析】
试题分析:∵A、B为锐角,sinA=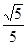 ,sinB=
,sinB=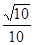 ,
,
∴cosA= =
= ,cosB=
,cosB=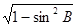 =
=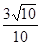 ,
,
∴cosC=-cos(A+B)=-(cosAcosB-sinAsinB)
=-( ×
×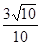 -
-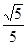 ×
×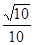 )=
)=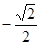 .
.
∵0<C<π,∴C=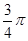 ---------------5分
---------------5分
(2)由(1)知C=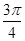 ,∴sinC=
,∴sinC=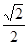 .
.
由正弦定理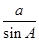 =
=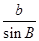 =
=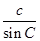 得
得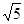 a=
a=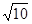 b=
b=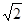 c,即a=
c,即a=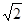 b,c=
b,c=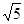 b,
b,
∵a-b=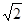 -1,∴
-1,∴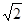 b-b=
b-b=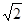 -1,∴b=1,
-1,∴b=1,
∴a=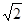 ,c=
,c=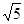 . ---------------10分
. ---------------10分
考点:本题考查正弦定理;诱导公式;三角形内的隐含条件。
点评:熟练掌握公式及定理是解本题的关键.在解题过程中,要仔细计算,避免出现计算错误。


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com