
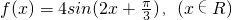 的图象关于点
的图象关于点 对称;
对称; .
. ≠45,因此不正确;
≠45,因此不正确;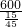 =1800,故正确;
=1800,故正确; =0,∴
=0,∴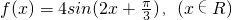 的图象关于点
的图象关于点 对称,故正确;
对称,故正确;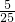 =
= ,故正确.
,故正确.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
| x |
| 2 |
| x |
| 2 |
| 2π |
| 9 |
| 2 |
| 2tanα |
| 1+tan2α |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
给出下列四个命题:
①sin2A=sin2B,则△ABC是等腰三角形;
②sin2=cosB,△ABC是直角三角形;
③cosAcosBcosC<0,则△ABC是钝角三角形;
④cos(A-B)cos(B-C)cos(C-A)=1,△ABC是等边三角形.
以上命题正确的为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:022
给出下列四个命题:
①sin2A=sin2B
,则△ABC是等腰三角形;②sin2=cosB
,△ABC是直角三角形;③cosAcosBcosC
<0,则△ABC是钝角三角形;④cos(A
-B)cos(B-C)cos(C-A)=1,△ABC是等边三角形.以上命题正确的为
___________.查看答案和解析>>
科目:高中数学 来源:甘肃省天水一中2011届高三第三次月考数学文科试题 题型:022
给出下列命题:
①当sin2![]() <0时,
<0时,![]() 是第二、第三象限角;
是第二、第三象限角;
②直线2x-3y-8=0与圆(x-1)2+(y+2)2=10一定相交;
③函数f(x)=x+![]() ,(x≥2)的最小值是2.
,(x≥2)的最小值是2.
其中真命题的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com