
(本题满分15分)已知数列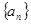 中,
中,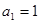 ,
,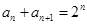 (n∈N*),
(n∈N*),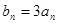
(1)试证数列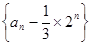 是等比数列,并求数列{
是等比数列,并求数列{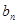 }的通项公式;
}的通项公式;
(2)在数列{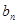 }中,求出所有连续三项成等差数列的项;
}中,求出所有连续三项成等差数列的项;
(3)在数列{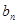 }中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
}中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
(1) (2)有且仅有连续三项b2,b3,b4成等差数列
(2)有且仅有连续三项b2,b3,b4成等差数列
(3)存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列
【解析】 解:(1)证明: 由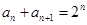 ,得an+1=2n—an,
,得an+1=2n—an,
∴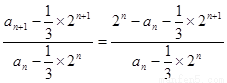
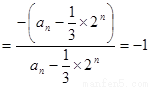 ,
,
∴数列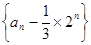 是首项为
是首项为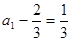 ,公比为
,公比为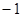 的等比数列.………………3分
的等比数列.………………3分
∴ 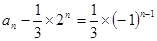 , 即
, 即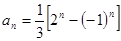 ,
,
∴ …………………………………………………………………………5分
…………………………………………………………………………5分
(2)解:假设在数列{bn}中,存在连续三项bk-1,bk,bk+1(k∈N*, k≥2)成等差数列,则bk-1+bk+1=2bk,即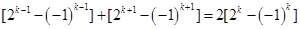 ,
,
即 =4
=4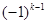 ………………………………………………………………7分
………………………………………………………………7分
若k为偶数,则 >0,4
>0,4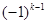 =-4<0,所以,不存在偶数k,使得
=-4<0,所以,不存在偶数k,使得
bk-1,bk,bk+1成等差数列。…………………………………………………………8分
若k为奇数,则k≥3,∴ ≥4,而4
≥4,而4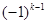 =4,所以,当且仅当k=3时,
=4,所以,当且仅当k=3时,
bk-1,bk,bk+1成等差数列。
综上所述,在数列{bn}中,有且仅有连续三项b2,b3,b4成等差数列。…………10分
(3)要使b1,br,bs成等差数列,只需b1+bs=2 br,
即3+ =2[
=2[ ],即
],即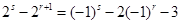 , ①
, ①
(ⅰ)若s=r+1,在①式中,左端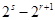 =0,右端
=0,右端 =
=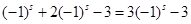 ,要使①式成立,当且仅当s为偶数时成立。又s>r>1,且s,r为正整数,所以,当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列。……………………………………………………………13分
,要使①式成立,当且仅当s为偶数时成立。又s>r>1,且s,r为正整数,所以,当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列。……………………………………………………………13分
(ⅱ)若s≥r+2时,在①式中,左端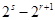 ≥
≥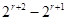 =
= >0,右端
>0,右端 ≤0,∴当s≥r+2时,b1,br,bs不成等差数列。
≤0,∴当s≥r+2时,b1,br,bs不成等差数列。
综上所述,存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列。…15分


科目:高中数学 来源:2013届浙江省余姚中学高三上学期期中考试文科数学试卷(带解析) 题型:解答题
(本题满分15分)已知点 (0,1),
(0,1), ,直线
,直线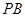 、
、 都是圆
都是圆 的切线(
的切线(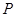 点不在
点不在 轴上).
轴上).
(Ⅰ)求过点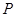 且焦点在
且焦点在 轴上的抛物线的标准方程;
轴上的抛物线的标准方程;
(Ⅱ)过点(1,0)作直线 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使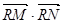 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省桐乡市高三10月月考理科数学 题型:解答题
(本题满分15分)已知函数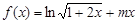 .
.
(Ⅰ)若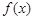 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;
(Ⅱ)当 时,求函数
时,求函数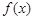 的最大值;
的最大值;
(Ⅲ)当 ,且
,且 时,证明:
时,证明: .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省桐乡市高三下学期2月模拟考试文科数学 题型:解答题
(本题满分15分)已知圆N: 和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B,
(1)当直线 的斜率为1时,求线段AB的长;
的斜率为1时,求线段AB的长;
(2)设点M和点N关于直线 对称,问是否存在直线
对称,问是否存在直线 使得
使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:杭州市2010年第二次高考科目教学质量检测 题型:解答题
(本题满分15分)已知直线 ,曲线
,曲线
(1)若 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值;
(2)若 ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com