
在△ 中,
中,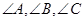 的对边分别为
的对边分别为 ,若
,若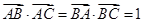 .
.
(1)求证: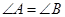 ;
;
(2)求边长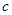 的值;
的值;
(3)若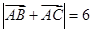 ,求△
,求△ 的面积.
的面积.
(1)详见解析;(2)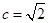 ;(3)
;(3)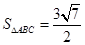 .
.
解析试题分析:(1)将条件中等式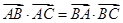 ,通过向量语言转化为角的等式,进而达到证明的目的;(2)结合条件自觉地选择余弦定理的恰当的表达形式,增加条件,从而解出边长
,通过向量语言转化为角的等式,进而达到证明的目的;(2)结合条件自觉地选择余弦定理的恰当的表达形式,增加条件,从而解出边长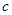 的值;(3)将向量等式
的值;(3)将向量等式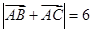 转化为边与角的等式,再结合(1)(2)可解出三边,进而可求出三角形的面积.在解三角形的问题中,关键是结合题目的自身特点,选择正、余弦定理的恰当形式,同时注意边角互化思想的使用.
转化为边与角的等式,再结合(1)(2)可解出三边,进而可求出三角形的面积.在解三角形的问题中,关键是结合题目的自身特点,选择正、余弦定理的恰当形式,同时注意边角互化思想的使用.
试题解析:(1)因为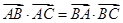 ,所以
,所以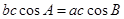 ,即
,即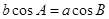 ,
,
由正弦定理得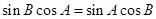 ,所以
,所以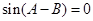 ,
,
因为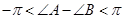 ,所以
,所以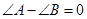 ,所以
,所以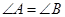 . 4分
. 4分
(2)由(1)知: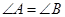 ,所以
,所以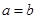 ,再由余弦定理得:
,再由余弦定理得: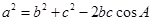 结合条件
结合条件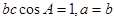 得:
得: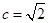 . 8分
. 8分
(3)由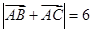 平方得:
平方得: ,又
,又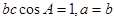 ,
,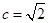 ,得
,得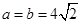 ,从而有
,从而有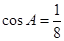 ,则
,则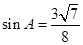 ,所以△
,所以△ 的面积为
的面积为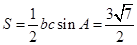 . 12分
. 12分
考点:向量数量积与解三角形综合.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com