练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （优选法与试验设计初步）某试验对象取值范围是[1，6]内的整数，采用分数法确定试点值，则第一个试点值可以是 ．

     

    4或3．

    【解析】

    试题分析：由题知试验范围为[1，6]，区间长度为5，故可把该区间等分成5段，利用分数法选取试点进行计算．

    【解析】
    由已知试验范围为[1，6]，可得区间长度为5，将其等分5段，

    利用分数法选取试点：x1=1+×（6﹣1）=4，x2=1+6﹣4=3，

    由对称性可知，第一次试点可以是4或3．

    故答案为：4或3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷（解析版） 题型：选择题

    （2014•深圳二模）过点（0，﹣1）的直线l与两曲线y=lnx和x2=2py均相切，则p的值为（ ）

    A. B. C.2 D.4

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教B版选修1-2 4.2结构图练习卷（解析版） 题型：选择题

    引入复数后，数系的结构图为（ ）

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教B版选修1-2 1.1独立性检验练习卷（解析版） 题型：选择题

    （2014•珠海二模）通过随机询问100名性别不同的小学生是否爱吃零食，得到如下的列联表：

     

    男

    女

    总计

    爱好

    10

    40

    50

    不爱好

    20

    30

    50

    总计

    30

    70

    100

     

    P（K2≥k）

    0.10

    0.05

    0.025

    k

    2.706

    3.841

    50.24

     

    由K2=算得K2=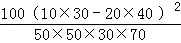≈4.762

    参照附表，得到的正确结论（ ）

    A.在犯错误的概率不超过5%的前提下，认为“是否爱吃零食与性别有关”

    B.在犯错误的概率不超过5%的前提下，认为“是否爱吃零食与性别无关”

    C.有97.5%以上的把握认为“是否爱吃零食与性别有关”

    D.有97.5%以上的把握认为“是否爱吃零食与性别无关”

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-7 1.4分数法练习卷（解析版） 题型：填空题

    那霉素发酵液生物测定，一般都规定培养温度为（37±1）℃，培养时间在16小时以上，某制药厂为了缩短时间，决定优选培养温度，试验范围固定在29～500C，精确度要求±1°C，用分数法安排实验，令第一试点在t1处，第二试点在t2处，则 t1+t2= ℃．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-7 1.4分数法练习卷（解析版） 题型：填空题

    （2012•湘潭三模）（优选法选做题）那霉素发酵液生物测定，一般都规定培养温度为（37±1）°C，培养时间在16小时以上，某制药厂为了缩短时间，决定优选培养温度，试验范围固定在32～45°C，精确度要求±1°C，用分数法安排实验，令第一试点在t1处，第二试点在t2处，则t1+t2= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-7 1.3黄金分割法-0.618法（解析版） 题型：填空题

    （优选法选讲）用0.618法对某一试验进行优选，存优范围是[2000，8000]，则第二个试点x2是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-7 1.3黄金分割法-0.618法（解析版） 题型：填空题

    （2012•长沙模拟）为了炼出某种特定用途的钢材，炼钢时需要加入一定量的某种化学元素，已知每炼1吨钢需要加入这种化学元素的量在[1000，2000]内（单位：g），采用0.618法确定最佳加入量，设第1，2，3个试点的加入最分别为x1，x22，x3（x1＞x2），若第1个试点比第2个试点好，则第3个试点的加入量x3= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 4.1信息的加密与去密练习卷（解析版） 题型：填空题

    为了保证信息安全传输，有一种称为秘密密钥密码系统，其加密、解密原理如下：

    明文密文密文明文

    现在加密密钥为y=loga（x+2），如上所示，明文“6”通过加密后得到密文“3”，再发送，接受方通过解密密钥解密得到明文“6”．问：若接受方接到密文为“4”，则解密后得到明文为（ ）

    A.12 B.13 C.14 D.15

     

    查看答案和解析>>

    同步练习册答案