
分析 由已知式子平方可得cosθ的方程,解方程可得.
解答 解:设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,
∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,
∴平方可得${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-2|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=|$\overrightarrow{a}$|2,
∴${\overrightarrow{b}}^{2}$=2|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=2|$\overrightarrow{b}$|2cosθ
∴cosθ=$\frac{1}{2}$
故答案为:$\frac{1}{2}$
点评 本题考查数量积和向量的夹角,属基础题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
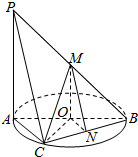 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{2}$] | B. | [$\frac{π}{2}$,π] | C. | [π,$\frac{3π}{2}$] | D. | [$\frac{3π}{2}$,2π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
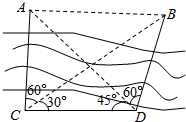 如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.
如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com