
设函数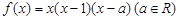 ,
,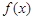 的两个极值点为
的两个极值点为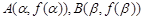 ,线段
,线段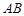 的中点为
的中点为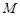 .
.
(1) 如果函数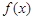 为奇函数,求实数
为奇函数,求实数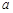 的值;当
的值;当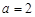 时,求函数
时,求函数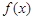 图象的对称中心;
图象的对称中心;
(2) 如果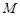 点在第四象限,求实数
点在第四象限,求实数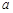 的范围;
的范围;
(3) 证明:点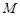 也在函数
也在函数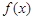 的图象上,且
的图象上,且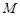 为函数
为函数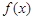 图象的对称中心.
图象的对称中心.
(1)函数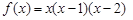 图象的对称中心为(1,0).
图象的对称中心为(1,0).
(2)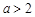 或
或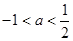 .
.
(3)由(2)得点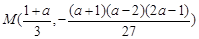 ,推出点
,推出点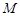 也在函数
也在函数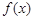 的图象上.
的图象上.
设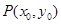 为函数
为函数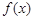 的图象上任意一点,
的图象上任意一点,
求得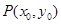 关于
关于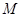 的对称点为
的对称点为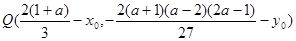
证明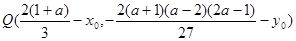 在函数
在函数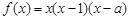 的图像上.证得
的图像上.证得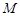 为函数
为函数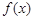 的对称中心.
的对称中心.
【解析】
试题分析:(1)【法一】因为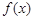 为奇函数,所以
为奇函数,所以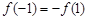 , 得:
, 得: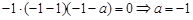 .
.
当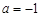 时,
时,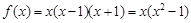 ,有
,有 ,则
,则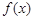 为奇函数. 4分
为奇函数. 4分
【法二】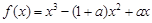 ,
, 恒成立,
恒成立, 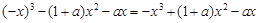 , 求得
, 求得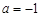 .
.
当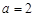 时,
时,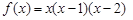 ,该图象可由奇函数
,该图象可由奇函数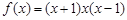 的图象向右平移一个单位得到, 可知函数
的图象向右平移一个单位得到, 可知函数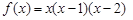 图象的对称中心为(1,0). 4分
图象的对称中心为(1,0). 4分
(2)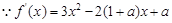 ,
,
令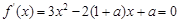 ,则
,则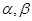 为
为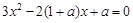 两实根.
两实根.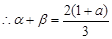 ,
,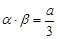 .
.
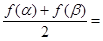
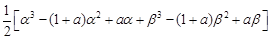
=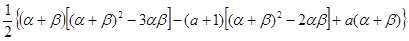
=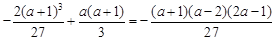 ,
,
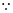 点
点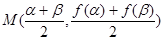 在第四象限,得:
在第四象限,得: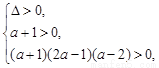
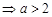 或
或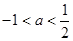 .
10分
.
10分
(3)由(2)得点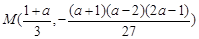 ,
,
又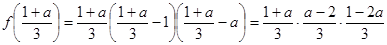
= ,所以点
,所以点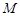 也在函数
也在函数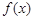 的图象上.
12分
的图象上.
12分
设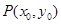 为函数
为函数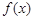 的图象上任意一点,
的图象上任意一点,
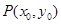 关于
关于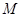 的对称点为
的对称点为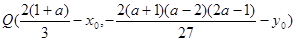
而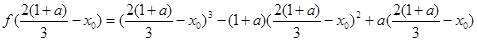
=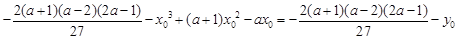 .
.
即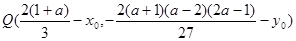 在函数
在函数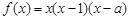 的图像上.
的图像上.
所以,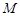 为函数
为函数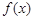 的对称中心.
16分
的对称中心.
16分
【法二】设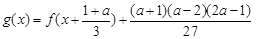
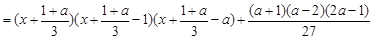
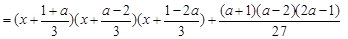
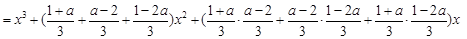
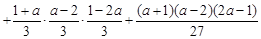
 .
.
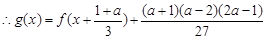 为奇函数,
为奇函数,
对称中心为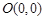 .
.
把函数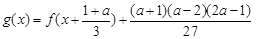 的图象按向量
的图象按向量
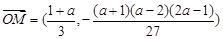 平移后得
平移后得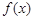 的图象,
的图象,
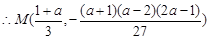 为函数
为函数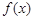 的对称中心.
16分
的对称中心.
16分
考点:本题主要考查函数的奇偶性,函数图象的对称性。
点评:中档题,本题解法较多,紧紧围绕函数图象的对称性展开讨论。奇函数图象关于原点对称,偶函数图象关于y轴对称。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 4 |
| a |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com