
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.
(1) ;(2)
;(2)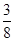 .
.
解析试题分析:(1)两张卡片的数字之和为奇数,即一奇一偶;两张卡片的数字之和为偶数,即两奇或两偶;(2)乙获胜,即要求乙取出的卡片上标有的数字比甲取出的卡片上标有的数字大,这样的情形有多少种,往往需要用枚举法.在(1)中我们是不考虑两张卡片的顺序的,若考虑顺序,即原题(1)这样表述:求乙随机先后抽取的两张卡片的数字之和为奇数的概率,则应这样求解:基本事件总数为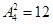 ,同时两张卡片的数字之和为奇数,即分为先奇后偶和先偶后奇,共
,同时两张卡片的数字之和为奇数,即分为先奇后偶和先偶后奇,共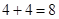 种,概率为
种,概率为 ,所以概率计算一定要分清与顺序是否有关.
,所以概率计算一定要分清与顺序是否有关.
试题解析:(1)乙随机在分别标有1、2、3、4的四张卡片中抽取的两张卡片,其基本事件共有 种,若要求两张卡片的数字之和为奇数,即一张为奇数,即在1、3中抽一张,另一张为偶数,即在2、4中抽一张,则两张卡片的数字之和为奇数这样的事件含有
种,若要求两张卡片的数字之和为奇数,即一张为奇数,即在1、3中抽一张,另一张为偶数,即在2、4中抽一张,则两张卡片的数字之和为奇数这样的事件含有 基本事件,根据古典概型概率计算公式的概率为
基本事件,根据古典概型概率计算公式的概率为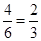 . 5分
. 5分
(2)甲、乙分别取出一张卡,则基本事件总数为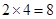 ,乙获胜,即要求乙取出的卡片上标有的数字比甲取出的卡片上标有的数字大,故符合条件的数对有
,乙获胜,即要求乙取出的卡片上标有的数字比甲取出的卡片上标有的数字大,故符合条件的数对有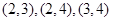 ,有3对,根据古典概型概率计算公式得乙获胜的概率为
,有3对,根据古典概型概率计算公式得乙获胜的概率为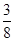 . 10分
. 10分
考点:计数原理与古典概型.


科目:高中数学 来源: 题型:解答题
在乒乓球比赛中,甲与乙以“五局三胜”制进行比赛,根据以往比赛情况,甲在每一局胜乙的概率均为  .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求:
(Ⅰ)甲在这种情况下取胜的概率;
(Ⅱ)设比赛局数为X,求X的分布列及数学期望(均用分数作答)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校夏令营有3名男同学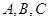 和3名女同学
和3名女同学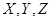 ,其年级情况如下表:
,其年级情况如下表:
| | 一年级 | 二年级 | 三年级 |
| 男同学 |  | 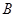 | 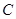 |
| 女同学 | 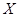 | 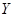 | 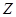 |
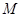 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件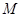 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下图是淮北市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择6月1日至6月15日中的某一天到达该市,并停留2天.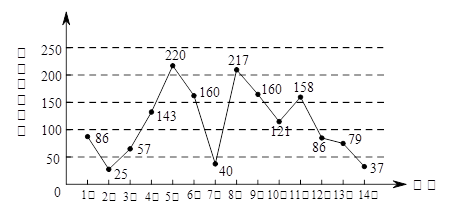
(1)求此人到达当日空气重度污染的概率;
(2)若设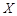 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
(3)由图判断从哪天开始淮北市连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
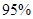 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?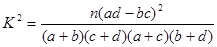 ,其中
,其中 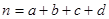
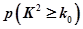 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为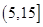 ,
,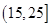 ,
,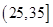 ,
,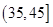 ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(1) 求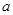 的值;
的值;
(2) 根据样本数据,试估计这一年度的空气质量指数的平均值;(注:设样本数据第 组的频率为
组的频率为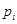 ,第
,第 组区间的中点值为
组区间的中点值为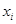
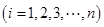 ,则样本数据的平均值为
,则样本数据的平均值为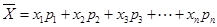 .)
.)
(3) 如果空气质量指数不超过 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取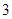 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为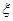 ,求
,求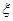 的分布列和数学期望.
的分布列和数学期望.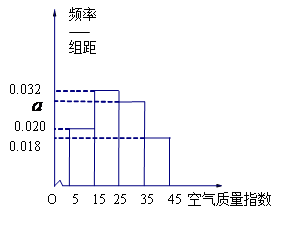
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数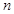 及天数如下表:
及天数如下表:
售出个数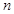 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
| | 不得禽流感 | 得禽流感 | 总计 |
| 服药 | | | |
| 不服药 | | | |
| 总计 | | | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com