
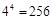 种.
种.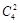 种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法:
种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法: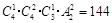 种.
种.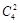 种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有
种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有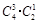 种放法;第二类:有
种放法;第二类:有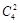 种放法.因此共有
种放法.因此共有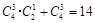 种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有:
种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有: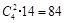 种.
种.

科目:高中数学 来源:不详 题型:单选题
| A.36种 | B.72种 | C.81种 | D.144种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
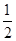 ,则质点P移动六次后位于点(4,2)的概率是 ( )
,则质点P移动六次后位于点(4,2)的概率是 ( )A. | B.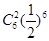 | C. | D.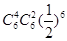 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.30种 | B.90种 | C.180种 | D.270种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
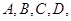 各棱长均为1米,有一个小虫从点
各棱长均为1米,有一个小虫从点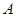 开始按以下规则前进:在每一顶点处用同样的概率选择通过这个顶点的三条棱之一,并一直爬到这条 棱的尽头,则它爬了
开始按以下规则前进:在每一顶点处用同样的概率选择通过这个顶点的三条棱之一,并一直爬到这条 棱的尽头,则它爬了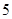 米之后恰好再次位于顶点
米之后恰好再次位于顶点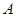 的概率是 (结果用分数表示).
的概率是 (结果用分数表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com