
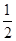 PD.
PD.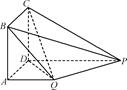
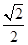 PD,则PQ⊥QD,又CD、QD为平面ADCB内两条相交直线,∴PQ⊥平面DCQ.
PD,则PQ⊥QD,又CD、QD为平面ADCB内两条相交直线,∴PQ⊥平面DCQ.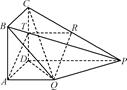
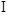 ?平面PDAQ,∴平面PDAQ⊥平面ABCD,交线为AD.又四边形ABCD为正方形,DC⊥AD,∴DC⊥平面PDAQ,可得PQ⊥DC.在直角梯形PDAQ中可得DQ=PQ=
?平面PDAQ,∴平面PDAQ⊥平面ABCD,交线为AD.又四边形ABCD为正方形,DC⊥AD,∴DC⊥平面PDAQ,可得PQ⊥DC.在直角梯形PDAQ中可得DQ=PQ=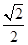 PD,则PQ⊥QD,又CD、QD为平面ADCB内两条相交直线,∴PQ⊥平面DCQ.
PD,则PQ⊥QD,又CD、QD为平面ADCB内两条相交直线,∴PQ⊥平面DCQ.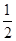 DP,又AQ∥DP,且AQ=
DP,又AQ∥DP,且AQ=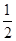 DP,从而AQ∥RT,且AQ=RT,∴四边形AQRT为平行四边形,所以AT∥QR,∵QR
DP,从而AQ∥RT,且AQ=RT,∴四边形AQRT为平行四边形,所以AT∥QR,∵QR 平面ABCD,AT
平面ABCD,AT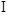 平面ABCD,∴QR∥平面ABCD.
平面ABCD,∴QR∥平面ABCD.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:单选题
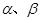 ,且
,且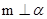 ,
,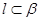 .给出下列命题:
.给出下列命题: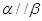 ,则
,则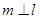 ;
;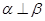 ,则
,则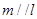 ;
;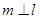 ,则
,则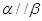 ;
;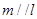 ,则
,则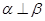 ,
,| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
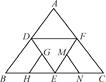
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
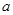 、
、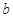 为不垂直的异面直线,
为不垂直的异面直线,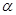 是一个平面,则
是一个平面,则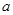 、
、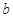 在
在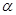 上的射影可能是:
上的射影可能是:查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
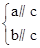 ⇒a∥b ②
⇒a∥b ② ⇒a∥b
⇒a∥b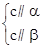 ⇒α∥β ④
⇒α∥β ④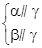 ⇒α∥β
⇒α∥β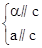 ⇒α∥a ⑥
⇒α∥a ⑥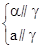 ⇒a∥α
⇒a∥α| A.①②③ | B.①④⑤ |
| C.①④ | D.①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com