已知数列{an}中,a1=1,且对于任意的正整数m,n都有am+n=aman+am+an,则数列{an}的通项公式为________.
2
n-1
分析:先根据条件得到a
n+1=a
na
1+a
n+a
1=2a
n+1;进而得到数列{a
n+1}是以a
1+1=2为首项,2为公比的等比数列;即可求出答案.
解答:因为数列{a
n}中,a
1=1,且对于任意的正整数m,n都有a
m+n=a
ma
n+a
m+a
n,
∴a
n+1=a
na
1+a
n+a
1=2a
n+1;
∴a
n+1+1=2(a
n+1);
∴
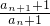
=2;
故数列{a
n+1}是以a
1+1=2为首项,2为公比的等比数列;
∴a
n+1=2×2
n-1=2
n.
∴a
n=2
n-1.
故答案为; 2
n-1.
点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,注意递推公式的合理运用.

 阅读快车系列答案
阅读快车系列答案