
分析 如图根据椭圆的性质可知,∠F1PF2当点P在短轴顶点(不妨设上顶点A)时最大,要椭圆上存在点P,满足∠F1PF2=120°,∠F1AF2≥120°,∠F1AO≥60°,即可,
解答 解:如图根据椭圆的性质可知,∠F1PF2当点P在短轴顶点(不妨设上顶点A)时最大,
要椭圆上存在点P,满足∠F1PF2=120°,
∠F1AF2≥120°,∠F1AO≥60°,sin∠F1AO=$\frac{c}{a}≥\frac{\sqrt{3}}{2}$,
故椭圆离心率的取范围是[$\frac{\sqrt{3}}{2}$,1)
故答案为[$\frac{\sqrt{3}}{2}$,1)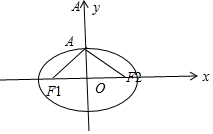
点评 本题考查了椭圆的离心率,借助平面几何知识是关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
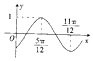 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{2}$)的值为( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{2}$)的值为( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
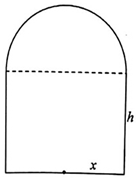 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com