
【题目】已知抛物线C:y2=2px(p>0)的焦点为F(1,0),抛物线E:x2=2py的焦点为M.
(1)若过点M的直线l与抛物线C有且只有一个交点,求直线l的方程;
(2)若直线MF与抛物线C交于A,B两点,求△OAB的面积.
【答案】见解析
【解析】
解:(1)由题意得抛物线C:y2=2px(p>0)的焦点为F(1,0),抛物线E:x2=2py的焦点为M,所以p=2,M(0,1),
①当直线l的斜率不存在时,x=0,满足题意;②当直线l的斜率存在时,设方程为y=kx+1,代入y2=4x,得k2x2+(2k-4)x+1=0,当k=0时,x=![]() ,满足题意,直线l的方程为y=1;当k≠0时,Δ=(2k-4)2-4k2=0,所以k=1,方程为y=x+1,综上可得,直线l的方程为x=0或y=1或y=x+1.
,满足题意,直线l的方程为y=1;当k≠0时,Δ=(2k-4)2-4k2=0,所以k=1,方程为y=x+1,综上可得,直线l的方程为x=0或y=1或y=x+1.
(2)结合(1)知抛物线C的方程为y2=4x,直线MF的方程为y=-x+1,
联立![]() 得y2+4y-4=0,
得y2+4y-4=0,
设A(x1,y1),B(x2,y2),
则y1+y2=-4,y1y2=-4,
所以|y1-y2|=4![]() ,
,
所以S△OAB=![]() |OF||y1-y2|=2
|OF||y1-y2|=2![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆的方程为![]() +
+![]() =1(a>b>0),右焦点为F(c,0)(c>0),方程ax2+bx-c=0的两实根分别为x1,x2,则P(x1,x2)( )
=1(a>b>0),右焦点为F(c,0)(c>0),方程ax2+bx-c=0的两实根分别为x1,x2,则P(x1,x2)( )
A.必在圆x2+y2=2内
B.必在圆x2+y2=2外
C.必在圆x2+y2=1外
D.必在圆x2+y2=1与圆x2+y2=2形成的圆环之间
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于155 cm到195 cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
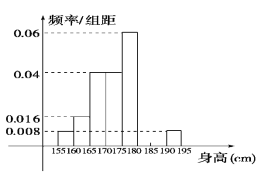
(Ⅰ)估计这所学校高三年级全体男生身高在180 cm以上(含180 cm)的人数;
(Ⅱ)求第六组、第七组的频率并补充完整频率分布直方图(用虚线标出高度);
(III)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为x、y,求事件“|x-y|≤5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的前n项和为Sn,已知对任意的n∈N*,点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图象上.
(1)求r的值;
(2)当b=2时,记bn=2(log2an+1)(n∈N*),证明:对任意的n∈N*,不等式![]() ·
·![]() ·…·
·…·![]() >
>![]() 成立.
成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com