
【题目】设椭圆的方程为![]() +
+![]() =1(a>b>0),右焦点为F(c,0)(c>0),方程ax2+bx-c=0的两实根分别为x1,x2,则P(x1,x2)( )
=1(a>b>0),右焦点为F(c,0)(c>0),方程ax2+bx-c=0的两实根分别为x1,x2,则P(x1,x2)( )
A.必在圆x2+y2=2内
B.必在圆x2+y2=2外
C.必在圆x2+y2=1外
D.必在圆x2+y2=1与圆x2+y2=2形成的圆环之间
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 分别交
分别交![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCDA1B1C1D1中,AB=AA1=1,E为BC中点.
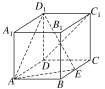
(1)求证:C1D⊥D1E;
(2)在棱AA1上是否存在一点M,使得BM∥平面AD1E?若存在,求![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若二面角B1AED1的大小为90°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心在原点,其一个焦点与抛物线y2=4![]() x的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.
x的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.

(1)求椭圆C的方程;
(2)当MA,MB与x轴所构成的三角形是以x轴上所在线段为底边的等腰三角形时,求直线l在y轴上截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F(1,0),抛物线E:x2=2py的焦点为M.
(1)若过点M的直线l与抛物线C有且只有一个交点,求直线l的方程;
(2)若直线MF与抛物线C交于A,B两点,求△OAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制药厂生产某种颗粒状粉剂,由医药代表负责推销,若每包药品的生产成本为![]() 元,推销费用为
元,推销费用为![]() 元,预计当每包药品销售价为
元,预计当每包药品销售价为![]() 元时,一年的市场销售量为
元时,一年的市场销售量为![]() 万包,若从民生考虑,每包药品的售价不得高于生产成本的
万包,若从民生考虑,每包药品的售价不得高于生产成本的![]() ,但为了鼓励药品研发,每包药品的售价又不得低于生产成本的
,但为了鼓励药品研发,每包药品的售价又不得低于生产成本的![]()
(1) 写出该药品一年的利润![]() (万元)与每包售价
(万元)与每包售价![]() 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
(2) 当每包药品售价![]() 为多少元时,年利润
为多少元时,年利润![]() 最大,最大值为多少?
最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每逢节假日,在微信好友群中发红包逐渐成为一种时尚,还能增进彼此的感情,2016年春节期间,小鲁在自己的微信好友群中,向在线的甲、乙、丙、丁四位好友随机发放红包,发放的规则为:每次发放一个,小鲁自己不抢,每个人抢到的概率相同.
(1)若小鲁随机发放了3个红包,求甲至少抢到一个红包的概率;
(2)若丁因有事暂时离线一段时间,而小鲁在这段时间内共发了3个红包,其中2个红包中各有10元,一个红包中有5元.设这段时间内乙所得红包的总钱数为![]() 元,求随机变量
元,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com