Question

19£®ÎÒÃÇ°ÑÀëÐÄÂÊe=$\frac{{\sqrt{5}+1}}{2}$µÄË«ÇúÏß$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1£¨{a£¾0£¬b£¾0}£©$³ÆΪ»Æ½ðË«ÇúÏߣ®¸ø³öÒÔϼ¸¸ö˵·¨£º
£¨1£©Ë«ÇúÏßx²-$\frac{{2{y^2}}}{{\sqrt{5}+1}}$=1ÊǻƽðË«ÇúÏߣ»
£¨2£©Èôb²=ac£¬Ôò¸ÃË«ÇúÏßÊǻƽðË«ÇúÏߣ»
£¨3£©ÈôMN¾­¹ýÓÒ½¹µãF₂ÇÒMN¡ÍF₁F₂£¬¡ÏMON=90¡ã£¬Ôò¸ÃË«ÇúÏßÊǻƽðË«ÇúÏߣ»
£¨4£©ÈôF₁£¬F₂Ϊ×óÓÒ½¹µã£¬A₁£¬A₂Ϊ×óÓÒ¶¥µã£¬B₁£¨0£¬b£©£¬B₂£¨0£¬-b£©ÇÒ¡ÏF₁B₁A₂=90¡ã£¬Ôò¸ÃË«ÇúÏßÊǻƽðË«ÇúÏߣ® ÆäÖÐÕýÈ·ÃüÌâµÄÐòºÅΪ£¨1£©£¨2£©£¨3£©£¨4£©£®

Answer 1

·ÖÎö £¨1£©ÀûÓÃË«ÇúÏߵļòµ¥ÐÔÖÊ·Ö±ðÇó³öÀëÐÄÂÊ£¬ÔÙÀûÓûƽðË«ÇúÏߵĶ¨ÒåÇó½â£®
£¨2£©Çó³öË«ÇúÏߵĶ¨ÒåÇó³öÀëÐÄÂÊ£¬¸ù¾Ý»Æ½ðË«ÇúÏߵĶ¨ÒåÇó½â£®
£¨3£©¸ù¾ÝÌõ¼þÇó³öË«ÇúÏߵĶ¨ÒåÇó³ö£¨2£©µÄ½áÂÛ£®
£¨4£©¸ù¾ÝÌõ¼þÇó³öÀëÐÄÂÊÇó³ö£¨2£©µÄ½áÂÛ£®

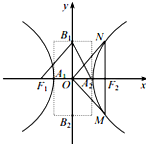½â´ð ½â£º£¨1£©Ë«ÇúÏßx²-$\frac{2{y}^{2}}{\sqrt{5}+1}$=1ÖУ¬$e=\frac{\sqrt{1+\frac{\sqrt{5}+1}{2}}}{1}=\frac{\sqrt{5}+1}{2}$
¡àË«ÇúÏßx²-$\frac{2{y}^{2}}{\sqrt{5}+1}$=1ÊǻƽðË«ÇúÏߣ¬¹Ê£¨1£©ÕýÈ·£»
¶ÔÓÚ£¨2£©¡ße¶ÔÓÚ£¨2£©b²=ac£¬Ôòe=$e=\frac{c}{a}=\frac{\sqrt{{a}^{2}+ac}}{a}=\sqrt{1+e}$¡àe²-e-1=0
½âµÃ$e=\frac{\sqrt{5}+1}{2}$»òe=$\frac{1-\sqrt{5}}{2}$£¨Éᣩ¡à¸ÃË«ÇúÏßÊǻƽðË«ÇúÏߣ¬¹Ê£¨2£©ÕýÈ·£»
¶ÔÓÚ£¨3£©Èçͼ£¬MN¾­¹ýÓÒ½¹µãF₂ÇÒMN¡ÍF₁F₂£¬¡ÏMON=90¡ã£¬
¡àNF₂=OF₂£¬¡à$\frac{{b}^{2}}{a}$=c£¬¡àb²=ac£¬
ÓÉ£¨2£©Öª¸ÃË«ÇúÏßÊǻƽðË«ÇúÏߣ¬¹Ê£¨3£©ÕýÈ·£®
¶ÔÓÚ£¨4£©Èçͼ£¬F₁£¬F₂Ϊ×óÓÒ½¹µã£¬A₁£¬A₂Ϊ×óÓÒ¶¥µã£¬
B₁£¨0£¬b£©£¬B₂£¨0£¬-b£©£¬ÇÒ¡ÏF₁B₁A₂=90¡ã£¬
¡àB₁F₁²+B₁A₂²=A₂F₁²£¬¼´b²+2c²=£¨a+c£©²£¬
ÕûÀí£¬µÃb²=ac£¬ÓÉ£¨2£©Öª¸ÃË«ÇúÏßÊǻƽðË«ÇúÏߣ¬¹Ê£¨4£©ÕýÈ·£»
¹Ê´ð°¸Îª£º£¨1£©£¨2£©£¨3£©£¨4£©£®

µãÆÀ ±¾Ì⿼²é»Æ½ðË«ÇúÏßµÄÅжϣ¬ÊÇÖеµÌ⣬½âÌâʱҪÈÏÕæÉóÌ⣬עÒâË«ÇúÏßµÄÐÔÖʵÄÁé»îÔËÓã®