
给定椭圆 .称圆心在原点O,半径为
.称圆心在原点O,半径为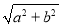 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为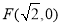 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为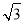 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线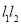 ,使得
,使得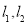 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断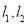 是否垂直?并说明理由.
是否垂直?并说明理由.
(1) 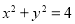 ; (2)
; (2) 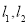 垂直.
垂直.
【解析】
试题分析:(1)由“椭圆C的一个焦点为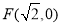 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为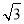 ”知:
”知: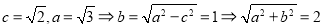 从而可得椭圆的标准方程和“准圆”的方程;
从而可得椭圆的标准方程和“准圆”的方程;
(2)分两种情况讨论:①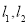 当中有一条直线斜率不存在;②直线
当中有一条直线斜率不存在;②直线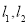 斜率都存在.
斜率都存在.
对于①可直接求出直线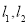 的方程并判断其是不互相垂直;
的方程并判断其是不互相垂直;
对于②设经过准圆上点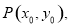 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为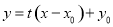
与椭圆方程联立组成方程组 消去
消去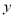 得到关于
得到关于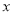 的方程:
的方程: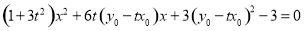
由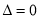 化简整理得:
化简整理得: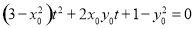
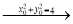
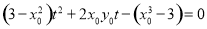
而直线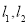 的斜率正是方程的两个根
的斜率正是方程的两个根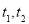 ,从而
,从而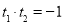
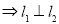
(1)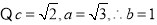
 椭圆方程为
椭圆方程为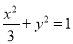
准圆方程为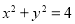
(2)①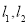 当中有一条无斜率时,不妨设
当中有一条无斜率时,不妨设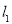 无斜率,
无斜率,
因为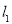 与椭圆只有一个共公点,则其方程为
与椭圆只有一个共公点,则其方程为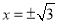
当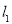 方程为
方程为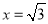 时,此时
时,此时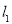 与准圆交于点
与准圆交于点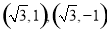
此时经过点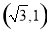 (或
(或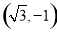 )且与椭圆只有一个公共眯的直线是
)且与椭圆只有一个公共眯的直线是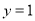 (或
(或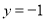 )
)
即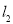 为
为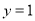 (或
(或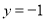 ),显然直线
),显然直线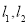 垂直;
垂直;
同理可证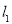 方程为
方程为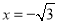 时,直线
时,直线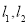 也垂直.
也垂直.
②当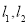 都有斜率时,设点
都有斜率时,设点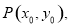 其中
其中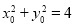
设经过点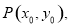 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为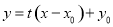
则由 消去
消去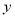 ,得
,得
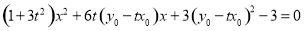
由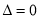 化简整理得:
化简整理得: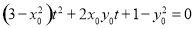
因为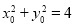 ,所以有
,所以有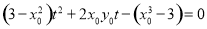
设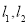 的斜率分别为
的斜率分别为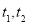 ,因为
,因为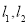 与椭圆只有一个公共点
与椭圆只有一个公共点
所以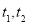 满足上述方程
满足上述方程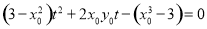
所以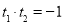 ,即
,即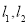 垂直,
垂直,
综合①②知, 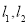 垂直.
垂直.
考点:1、椭圆的标准方程;2、直线与圆锥曲线的综合问题.


科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷文科数学试卷(解析版) 题型:选择题
没函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对一切实数x均成 立,则称
对一切实数x均成 立,则称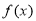 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:①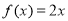 :②
:②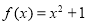 :③
:③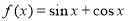 ;④
;④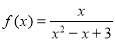 ⑤
⑤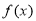 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切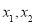 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
A.1个 B.2个 C..3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模理科数学试卷(解析版) 题型:填空题
三棱柱的直观图和三视图(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所永,则这个三棱柱的全面积等于_____________
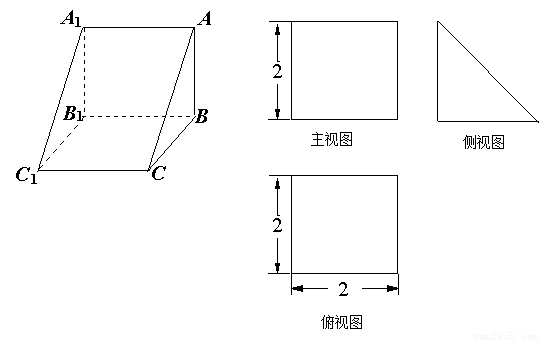
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模文科数学试卷(解析版) 题型:填空题
在平行四边形ABCD中,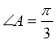 ,边AB、 AD的长分别为2,1,若M、N分别是边BC、CD上的点,且满足
,边AB、 AD的长分别为2,1,若M、N分别是边BC、CD上的点,且满足 ,则
,则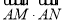 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模文科数学试卷(解析版) 题型:选择题
已知棱长为l的正方体 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A. 面ABCD
面ABCD
B. AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时, 不是定直线
不是定直线
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市南开区高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知下列三个命题:
①棱长为2的正方体外接球的体积为4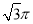 ;
;
②如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
③直线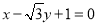 被圆
被圆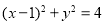 截得的弦长为2
截得的弦长为2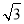 .
.
其中真命题的序号是( )。
(A)①② (B)②③ (C)①③ (D)①②③
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考文科数学试卷(解析版) 题型:解答题
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.

(1)证明:BC1//平面A1CD;
(2)设AA1=AC=CB=2,AB= ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com