
在直角坐标系中,射线OA: x-y=0(x≥0),
OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
(1)当AB中点为P时,求直线AB的方程;
(2)当AB中点在直线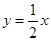 上时,求直线AB的方程.
上时,求直线AB的方程.
(1)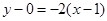 ,即
,即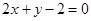 (2)
(2)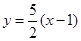
【解析】本试题主要是考查了直线的方程的求解,以及对称点的坐标运用。
(1)因为射线OA: x-y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点,结合中点公式得到交点的坐标。进而得到直线方程
(2)分别对于直线AB斜率存在与否进行分类讨论,然后联立方程组的思想得到交点坐标,利用中点公式得到结论。
解:(1)因为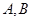 分别为直线与射线
分别为直线与射线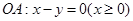 及
及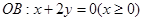 的交点,
所以可设
的交点,
所以可设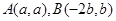 ,又点
,又点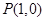 是
是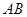 的中点,
的中点,
所以有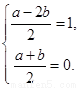 即
即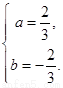 ∴A、B两点的坐标为
∴A、B两点的坐标为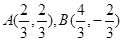 ,……4分
,……4分
∴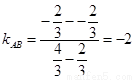 ,……….5分
,……….5分
所以直线AB的方程为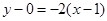 ,即
,即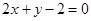 ………..6分
………..6分
(2)①当直线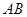 的斜率不存在时,则
的斜率不存在时,则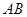 的方程为
的方程为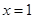 ,易知
,易知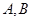 两点的坐标分别为
两点的坐标分别为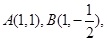 所以
所以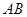 的中点坐标为
的中点坐标为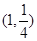 ,显然不在直线
,显然不在直线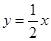 上,
上,
即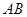 的斜率不存在时不满足条件. ……….8分
的斜率不存在时不满足条件. ……….8分
②当直线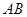 的斜率存在时,记为
的斜率存在时,记为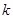 ,易知
,易知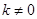 且
且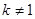 ,则直线
,则直线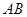 的方程为
的方程为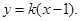
分别联立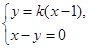 及
及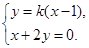
可求得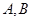 两点的坐标分别为
两点的坐标分别为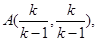
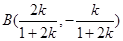
所以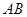 的中点坐标为
的中点坐标为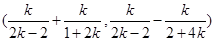 ……….10分
……….10分
又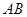 的中点在直线
的中点在直线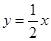 上,所以
上,所以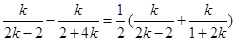 解得
解得
所以直线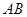 的方程为
的方程为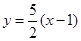 ,即
,即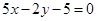 …………13分
…………13分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
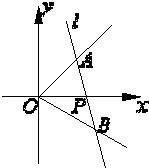 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届安徽合肥一六八中学高二上学期期中考试文数学卷(解析版) 题型:解答题
如图,在直角坐标系中,射线OA: x-y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
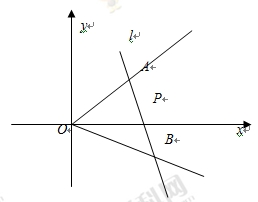
(1)当AB中点为P时,求直线AB的斜率
(2)当AB中点在直线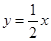 上时,求直线AB的方程.
上时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2014届福建省高一第一学期期末考试数学试卷 题型:解答题
如图,在直角坐标系中,射线 :
: ,
, :
: ,
,
过点 作直线分别交射线
作直线分别交射线 、
、 于
于 、
、 点.
点.
(1)当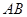 的中点为
的中点为 时,求直线
时,求直线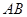 的方程;
的方程;
(2)当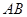 的中点在直线
的中点在直线 上时,求直线
上时,求直线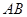 的方程.
的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com