
曲线 在区间
在区间 上截直线
上截直线 及
及 所得的弦
所得的弦
长相等且不为 ,则下列对
,则下列对 的描述正确的是( )
的描述正确的是( )
A. | B. | C. | D. |
A
解析试题分析:曲线y=Asinωx+a(A>0,ω>0)的性质知,在一个周期上截直线y=2与y=-1所得的弦长相等且不为0,可知两条直线关于y=a对称,由此对称性可求出a,又截得的弦长不为0,故可得振幅大于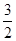 .解:由题意曲线y=Asinωx+a(A>0,ω>0)的图象关于直线y=a的对称,截直线y=2及y=-1所得的弦长相等,以,两条直线y=2及y=-1关于y=a对称, a=
.解:由题意曲线y=Asinωx+a(A>0,ω>0)的图象关于直线y=a的对称,截直线y=2及y=-1所得的弦长相等,以,两条直线y=2及y=-1关于y=a对称, a=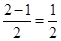 =
=
又弦长相等且不为0,故振幅A大于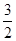 ,A>
,A>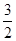 故有a=
故有a=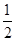 ,A>
,A>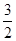 ,应选A.
,应选A.
考点:y=Asin(ωx+φ)中参数意义
点评:本题考点y=Asin(ωx+φ)中参数的物理意义,考查三角函数的图象的性质及其与相应参数的关系,考查对三角函数图象的特征理解的能力


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:单选题
函数f(x)=M sin (ωx+φ),(ω>0) 在区间 [ a , b ] 上是增函数,且f(a)=-M,f(b)=M,则函数g(x)=M cos (ωx+φ) 在 [ a , b ] 上( )
| A.增函数 | B.是减函数 | C.可以取最大值M | D.可以取最小值-M |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com