
过双曲线 的左焦点F(-c,0)(c >0),作圆:
的左焦点F(-c,0)(c >0),作圆: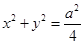 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若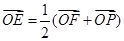 ,则双曲线的离心率为
,则双曲线的离心率为
A.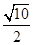 B.
B.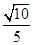 C.
C.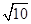 D.
D.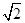
 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第七次阶段复习达标检测理科数学试卷(解析版) 题型:填空题
过双曲线 的左焦点F作⊙O:
的左焦点F作⊙O:  的两条切线,记切点为A,B,双曲线左顶点为C,若
的两条切线,记切点为A,B,双曲线左顶点为C,若 ,则双曲线的离心率为____________.
,则双曲线的离心率为____________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省五校高三第四次联考数学理卷 题型:选择题
过双曲线
 的左焦点F的直线
的左焦点F的直线 与双曲线的左支交于A、B两点,且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为
与双曲线的左支交于A、B两点,且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为 ,那么双曲线的离心率为
,那么双曲线的离心率为
(A) (B)
(B) (C)2 (D)
(C)2 (D)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省五校高三第四次联考数学理卷 题型:选择题
过双曲线
 的左焦点F的直线
的左焦点F的直线 与双曲线的左支交于A、B两点,且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为
与双曲线的左支交于A、B两点,且以线段AB为直径的圆被双曲线C的左准线截得的劣弧的弧度数为 ,那么双曲线的离心率为
,那么双曲线的离心率为
(A) (B)
(B) (C)2 (D)
(C)2 (D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com