
已知函数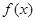 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
.
(1)求函数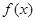 的解析式;
的解析式;
(2)解不等式 ;
;
(3)若函数 在区间
在区间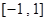 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
(1)  ;(2) 解集为
;(2) 解集为 ;(3)
;(3)  .
.
【解析】
试题分析:(1)两个函数的图象关于某点或某条直线对称,一般设待求解析式的函数图象上任一点的坐标为 ,求出这点的对称点的坐标
,求出这点的对称点的坐标 ,当然这里
,当然这里 是用
是用 表示的式子,然后把点
表示的式子,然后把点 代入已知解析式,就能求出结论;(2)这是含有绝对值的不等式,解题时,一般按照绝对值的定义分类讨论以去掉绝对值符号,便于解题;(3)
代入已知解析式,就能求出结论;(2)这是含有绝对值的不等式,解题时,一般按照绝对值的定义分类讨论以去掉绝对值符号,便于解题;(3)  ,这是含参数的二次函数,解题时,首先对二次项系数
,这是含参数的二次函数,解题时,首先对二次项系数 分类,即分二次项系数
分类,即分二次项系数 为0,不为0,其中
为0,不为0,其中 不为0还要分为是正数,还是负数进行讨论,在二次项系数
不为0还要分为是正数,还是负数进行讨论,在二次项系数 不为0时,只要讨论其对称轴与给定区间的关系就能求得结论.
不为0时,只要讨论其对称轴与给定区间的关系就能求得结论.
试题解析:(1)设 是函数
是函数 图像上任一点,则
图像上任一点,则 关于原点对称的点
关于原点对称的点 在函数
在函数 的图像上,
(1分)
的图像上,
(1分)
所以 ,故
,故 . (2分)
. (2分)
所以,函数 的解析式是
的解析式是 . (1分)
. (1分)
(2)由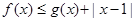 ,得
,得 , (1分)
, (1分)
即 . (1分)
. (1分)
当 时,有
时,有 ,△
,△ ,不等式无解; (1分)
,不等式无解; (1分)
当 时,有
时,有 ,
, ,解得
,解得 . (2分)
. (2分)
综上,不等式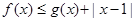 的解集为
的解集为 . (1分)
. (1分)
(3) . (1分)
. (1分)
①当 时,
时, 在区间
在区间 上是增函数,符合题意. (1分)
上是增函数,符合题意. (1分)
②当 时,函数
时,函数 图像的对称轴是直线
图像的对称轴是直线 . (1分)
. (1分)
因为 在区间
在区间 上是增函数,所以,
上是增函数,所以,
1)当 时,
时, ,函数
,函数 图像开口向上,故
图像开口向上,故 ,
,
解得 ; (1分)
; (1分)
2)当 时,
时,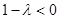 ,函数
,函数 图像开口向下,故
图像开口向下,故 ,解得
,解得 .
(1分)
.
(1分)
综上, 的取值范围是
的取值范围是 . (1分)
. (1分)
考点:(1)函数图象的对称问题;(2)含绝对值的不等式;(3)函数的单调性.


科目:高中数学 来源:2012-2013学年重庆市重庆一中高二下学期期中考试文科数学试卷(带解析) 题型:填空题
已知命题 :“函数
:“函数 和
和 的图像关于
的图像关于 轴对称”,则
轴对称”,则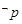 是 命题;(填“真”或“假” )
是 命题;(填“真”或“假” )
查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市高三上学期第一次月考理科数学试卷(解析版) 题型:解答题
已知函数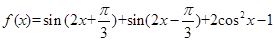 ,
, .
.
 求函数
求函数 的最小正周期;
的最小正周期;
 若函数
若函数 的图像和
的图像和 的图像关于直线
的图像关于直线 对称,求
对称,求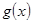 在
在 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com