
设a=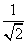 (sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
(sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
c=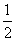 (cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
(cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
A.a>b>c B.b>a>c C.c>a>b D.a>c>b
科目:高中数学 来源: 题型:
在△ABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5,sinB=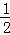 .
.
(1)求sinA和cosC的值;
(2)设函数f(x)=sin(x+2A),求f(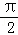 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如果某年年份的各位数字之和为7,我们称该年为“七巧年”.例如,今年年份2014的各位数字之和为7,所以今年恰为“七巧年”,那么从2000年到2999年中“七巧年”共有 _________ 个.
查看答案和解析>>
科目:高中数学 来源: 题型:
在(1+x+x2)n=D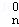 +D
+D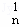 x+D
x+D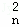 x2+…+D
x2+…+D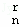 xr+…+D
xr+…+D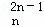 x2n﹣1+D
x2n﹣1+D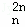 x2n的展开式中,把D
x2n的展开式中,把D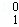 ,D
,D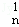 ,D
,D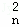 ,…,D
,…,D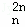 叫做三项式系数.
叫做三项式系数.
(1)当n=2时,写出三项式系数D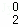 ,D
,D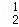 ,D
,D ,D
,D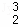 ,D
,D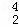 的值;
的值;
(2)类比二项式系数性质C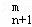 =C
=C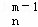 +C
+C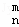 (1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D
(1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D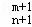 (1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(3)求D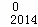 C
C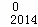 ﹣D
﹣D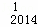 C
C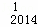 +D
+D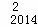 C
C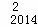 ﹣
﹣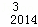 C
C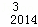 +…+D
+…+D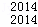 C
C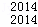 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com