
在(1+x+x2)n=D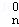 +D
+D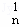 x+D
x+D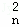 x2+…+D
x2+…+D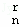 xr+…+D
xr+…+D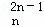 x2n﹣1+D
x2n﹣1+D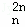 x2n的展开式中,把D
x2n的展开式中,把D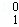 ,D
,D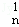 ,D
,D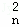 ,…,D
,…,D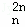 叫做三项式系数.
叫做三项式系数.
(1)当n=2时,写出三项式系数D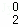 ,D
,D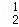 ,D
,D ,D
,D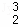 ,D
,D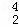 的值;
的值;
(2)类比二项式系数性质C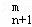 =C
=C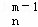 +C
+C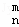 (1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D
(1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D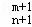 (1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(3)求D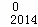 C
C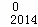 ﹣D
﹣D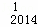 C
C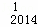 +D
+D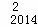 C
C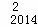 ﹣
﹣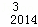 C
C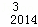 +…+D
+…+D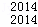 C
C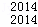 的值.
的值.
解:(1)因为(1+x+x2)2=x4+2x3+3x2+2x+1,
所以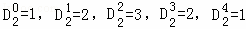 .
.
(2)类比二项式系数性质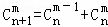 (1≤m≤n,m∈N,n∈N),三项式系数有如下性质:
(1≤m≤n,m∈N,n∈N),三项式系数有如下性质: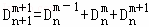 ,(1≤m≤2n﹣1)
,(1≤m≤2n﹣1)
因为(1+x+x2)n+1=(1+x+x2)•(1+x+x2)n,
所以(1+x+x2)n+1=(1+x+x2)•(D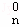 +D
+D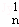 x+D
x+D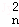 x2+…+D
x2+…+D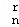 xr+…+D
xr+…+D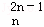 x2n﹣1+D
x2n﹣1+D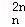 x2n).
x2n).
上式左边xm+1的系数为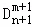 ,
,
而上式右边xm+1的系数为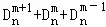 ,
,
由(1+x+x2)n+1=(1+x+x2)•(1+x+x2)n为恒等式,得
: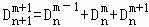 ,(1≤m≤2n﹣1);
,(1≤m≤2n﹣1);
(3)∵(1+x+x2)2014=D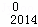 x0﹣D
x0﹣D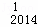 x1+D
x1+D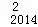 x2﹣D
x2﹣D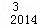 x3+…+D
x3+…+D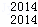 x2014,
x2014,
(x﹣1)2014=C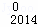 x2014﹣C
x2014﹣C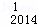 x2013+C
x2013+C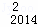 x2012﹣…+C
x2012﹣…+C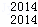 .
.
∴(1+x+x2)2014(x﹣1)2014中x2014系数为D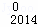 C
C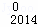 ﹣D
﹣D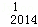 C
C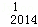 +D
+D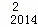 C
C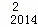 ﹣D
﹣D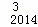 C
C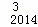 +…+D
+…+D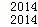 C
C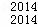 ,
,
又∴(1+x+x2)2014(x﹣1)2014=(x3﹣1)2014
而二项式(x3﹣1)2014 的通项 ,
,
因为2014不是3的倍数,所以(x3﹣1)2014 的展开式中没有x2014项,
由代数式恒成立,得
D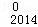 C
C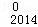 ﹣D
﹣D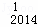 C
C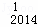 +D
+D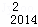 C
C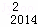 ﹣D
﹣D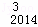 C
C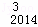 +…+D
+…+D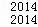 C
C =0.
=0.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
已知极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的非负半轴重合,且长度单位相同,若圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为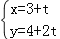 (t为参数),直线l与圆C交于A,B两点.
(t为参数),直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)求AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a=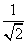 (sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
(sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
c=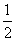 (cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
(cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
A.a>b>c B.b>a>c C.c>a>b D.a>c>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com