
已知极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的非负半轴重合,且长度单位相同,若圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为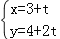 (t为参数),直线l与圆C交于A,B两点.
(t为参数),直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)求AB的长.
科目:高中数学 来源: 题型:
函数f(x)在定义域R内可导,若f(x)=f(2﹣x),且(x﹣1)f′(x)>0,若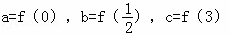 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
|
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一门高射炮射击一次击中目标的概率是0.4,那么至少需要这样的高射炮多少门同时对某一目标射击一次,才能使该目标被击中的概率超过96%(提供的数据: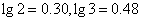 )
)
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军,若两队胜每局的概率相同,则甲队获得冠军的概率为 _________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
在(1+x+x2)n=D +D
+D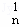 x+D
x+D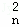 x2+…+D
x2+…+D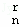 xr+…+D
xr+…+D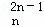 x2n﹣1+D
x2n﹣1+D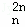 x2n的展开式中,把D
x2n的展开式中,把D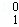 ,D
,D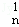 ,D
,D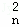 ,…,D
,…,D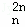 叫做三项式系数.
叫做三项式系数.
(1)当n=2时,写出三项式系数D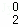 ,D
,D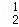 ,D
,D ,D
,D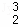 ,D
,D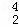 的值;
的值;
(2)类比二项式系数性质C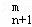 =C
=C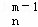 +C
+C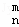 (1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D
(1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D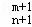 (1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(3)求D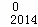 C
C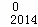 ﹣D
﹣D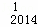 C
C +D
+D C
C ﹣
﹣ C
C +…+D
+…+D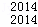 C
C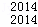 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com