函数f（x）在定义域R内可导，若f（x）=f（2﹣x），且（x﹣1）f′（x）＞0，若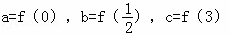
，则a，b，c的大小关系是（ ）
|
| A． | a＞b＞c | B． | c＞a＞b | C． | b＞a＞c | D． | c＞b＞a |
科目：高中数学 来源： 题型：
在△ABC中，a、b、c分别为角A、B、C所对的边，且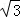
c=2bsinC
（Ⅰ）试确定角B的大小；
（Ⅱ）若△ABC为锐角三角形，b=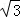，求a+c的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
用反证法证明命题“：若 a，b∈N，ab能被3整除，那么a，b中至少有一个能被3整除”时，假设应为（ ）
|
| A． | a，b都能被3整除 | B． | a不能被3整除 |
|
| C． | a，b不都能被3整除 | D． | a，b都不能被3整除 |
查看答案和解析>>
科目：高中数学 来源： 题型：
已知抛物线C1：y2=8x与双曲线C2：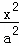
﹣
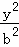=1（a＞0，b＞0）有公共焦点F2．点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（1）求双曲线交点F2及另一交点F1的坐标和点A的坐标；
（2）求双曲线C2的方程；
（3）以F1为圆心的圆M与直线y=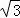
x相切，圆N：（x﹣2）2+y2=1，过点P（1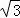，）作互相垂直且分别与圆M、圆N相交的直线l1和l2，设l1被圆M截得的弦长为s，l2被圆N截得的弦长为t，问：
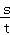是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
为了调查喜爱运动是否和性别有关，我们随机抽取了50名对象进行了问卷调查得到了如下的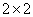
列联表:
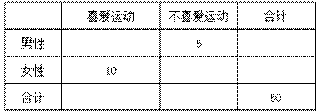
若在全部50人中随机抽取2人,抽到喜爱运动和不喜爱运动的男性各一人的概率为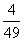
.
(1)请将上面的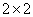列联表补充完整；
(2)能否在犯错误的概率不超过0.001的前提下认为喜爱运动与性别有关?说明你的理由.
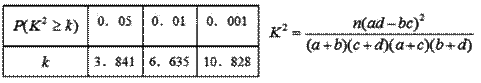附:
查看答案和解析>>
科目：高中数学 来源： 题型：
已知极坐标系的极点在平面直角坐标系的原点O处，极轴与x轴的非负半轴重合，且长度单位相同，若圆C的极坐标方程为ρ=2cosθ，直线l的参数方程为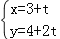
（t为参数），直线l与圆C交于A，B两点．
（1）求圆C的直角坐标方程与直线l的普通方程；
（2）求AB的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＜
，
），那么它的直角坐标系表示为 _________ ．