练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军，若两队胜每局的概率相同，则甲队获得冠军的概率为　_________　．

    　



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     用反证法证明命题“：若 a，b∈N，ab能被3整除，那么a，b中至少有一个能被3整除”时，假设应为（　　）

    　

    A．

    a，b都能被3整除

    B．

    a不能被3整除

    　

    C．

    a，b不都能被3整除

    D．

    a，b都不能被3整除

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列推理过程是演绎推理的是                                          

    A．由平面三角形的性质推测空间三棱锥的性质

    B．某校高二1班有55人，2班有52人，由此得高二所有班人数都超过50人

    C．两条直线平行，同位角相等；若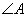与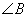是两条平行直线的同位角，则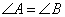

    D．在数列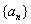中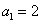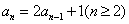，，，由此归纳出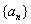的通项公式

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司在一次年会上举行了有奖问答活动，会议组织者准备了10道题目，其中6道选择题,4道填空题,公司一职员从中任取3道题解答.

    (1)求该职员至少取到1道填空题的概率；

    (2)已知所取的3道题中有2道选择题,道填空题.设该职员答对选择题的概率都是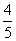,答对每道填空题的概率都是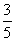,且各题答对与否相互独立.用表示该职员答对题的个数,求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若离散型随机变量X～B（6，p），且E（X）=2，则p=　_________　．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知极坐标系的极点在平面直角坐标系的原点O处，极轴与x轴的非负半轴重合，且长度单位相同，若圆C的极坐标方程为ρ=2cosθ，直线l的参数方程为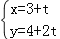（t为参数），直线l与圆C交于A，B两点．

    （1）求圆C的直角坐标方程与直线l的普通方程；

    （2）求AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知e1，e2是夹角为60°的两个单位向量，若a＝e1＋e2，b＝－4e1＋2e2，则a与b的

    夹角为                                                           (    )

    A．30°             B．60°             C．120°           D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}各项均为正数，其前n项和为Sn，且满足4Sn=(an+1)2.

    (1)求{an}的通项公式；

    (2)设bn=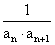，数列{bn}的前n项和为Tn,求Tn的最小值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆的圆心坐标和半径分别是         

    查看答案和解析>>

    同步练习册答案