(1)证明::(1)∵a
1+2a
2+3a
3+…+na
n=
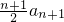
①,
∴n≥2时,a
1+2a
2+3a
3+…+(n-1)a
n-1=
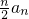
②
①-②得na
n=
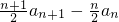
3na
n=(n+1)a
n+1即
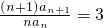
∵a
1=1,∴a
2=1
∴
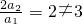
∴n≥2时,数列{na
n}为等比数列
(2)由(1)可得na
n=
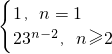
∴
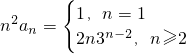
则当n=1时,T
1=1
∴当n≥2时,
T
n=1+2[2×3
0+3×3
1+…+n×3
n-2]
3T
n=3+2[2×3
1+3×3
2+…+(n-1)•3
n-2+n•3
n-1]
相减得2T
n=2+2[n•3
n-1-(2+3+3
2+2
3+…+3
n-2)]=(2n-1)3
n-1+1(n≥2)
T
n=
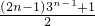
(n≥2)
又T
1=1,符合T
n的形式,
∴T
n=

(2n-1)•3
n+1(n∈N
*)
分析:(1)根据题意,可得a
1+2a
2+3a
3+…+na
n-1=
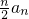
,两者相减,整理可得
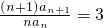
,从而可得数列{a
n}为等比数列
(2)根据题意,求出n
2a
n通项公式,利用错位相减可求数列的和
点评:本题主要考查了等比数列的通项公式的求解,数列求和的错位相减求和是数列求和中的重点与难点,要注意掌握

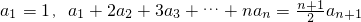 (n∈N*).
(n∈N*).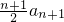 ①,
①,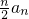 ②
②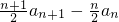
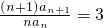
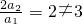
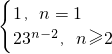
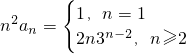
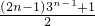 (n≥2)
(n≥2) (2n-1)•3n+1(n∈N*)
(2n-1)•3n+1(n∈N*)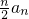 ,两者相减,整理可得
,两者相减,整理可得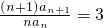 ,从而可得数列{an}为等比数列
,从而可得数列{an}为等比数列
