
分析 (1)根据向量的数量积公式和三角形函数的化简求出f(x),再求出对称轴方程和对称中心坐标,
(2)根据图象的变换可得g(x),再根据正弦函数的性质求出函数的值域.
解答 解:(1)∵$\overrightarrow m=({sinx,1}),\overrightarrow{\;n}=({\sqrt{3}Acosx,\frac{A}{2}cos2x})({A>0})$,
∴$f(x)=\overrightarrow m•\overrightarrow n$=$\sqrt{3}$Asinxcosx+$\frac{A}{2}$cos2x=Asin(2x+$\frac{π}{6}$),
∵函数$f(x)=\overrightarrow m•\overrightarrow n$的最大值为6,
∴A=6,
∴对称轴方程为$x=\frac{π}{6}+\frac{kπ}{2}\;,\;k∈Z$,对称中心坐标为$(-\frac{π}{12}+\frac{kπ}{2},0),k∈Z$;
(2)∵函数y=f(x)的图象向左平移$\frac{π}{12}$个单位,
再将所得的图象上各点的横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标不变,
∴$g(x)=6sin(4x+\frac{π}{3})$,
∵x∈$[{0,\frac{5π}{24}}]$,
∴4x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],
∴sinx∈[-$\frac{1}{2}$,1],
∴值域为[-3,6].
点评 本题考查了平面向量的数量积及三角函数的化简与其性质的应用,属于中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
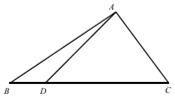 如图,在△ABC中,点D在BC边上,α=∠BAD,(1+tanα)(1+tanβ)=2,cosC=$\frac{3}{5}$.
如图,在△ABC中,点D在BC边上,α=∠BAD,(1+tanα)(1+tanβ)=2,cosC=$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点.
如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com