Question

设项数为奇数的等差数列，奇数项之和为44，偶数项之和为33，求这个数列的中间项及项数．

Answer 1

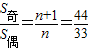
【答案】分析：设等差数列{a_n}项数为2n+1，根据等差数列的性质可得∴，解得n=3，因为S_奇-S_偶=a_n+1=a_中，所以a₄=S_奇-S_偶=44-33=11．
解答：解：设等差数列{a_n}项数为2n+1，
S_奇=a₁+a₃+…+a_2n+1=，
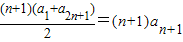
S_偶=a₂+a₄+a₆+…+a_2n=，
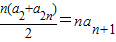
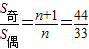
∴，解得n=3，
∴项数2n+1=7，
又因为S_奇-S_偶=a_n+1=a_中，
所以a₄=S_奇-S_偶=44-33=11，
所以中间项为11．
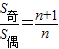
点评：解决此类问题的关键是熟练掌握等差数列的有关性质，如等差数列的项数为项数为2n+1时，并且S_奇-S_偶=a_n+1=a_中．