
科目:高中数学 来源:不详 题型:解答题
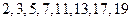 八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
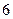 人中选出
人中选出 名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.
名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 若
若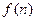 的取值集合为{165,168,170,173,175,177}(单位:cm)则满足
的取值集合为{165,168,170,173,175,177}(单位:cm)则满足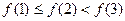 的所有可能的结果种数为( )
的所有可能的结果种数为( )| A.35 | B.30 | C.20 | D.15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com