
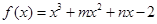 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数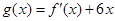 的图象关于y轴对称.
的图象关于y轴对称.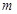 、
、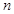 的值及函数
的值及函数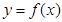 的单调区间;
的单调区间;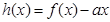 在(-1,1)上单调递减,求实数
在(-1,1)上单调递减,求实数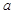 的取值范围。
的取值范围。 =0,所以m=-3,代入①得n=0.
=0,所以m=-3,代入①得n=0. 在(-1,1)上恒成立,得a≥3x2-6x对x∈(-1,1)恒成立. ∵-1<x<1,∴3x2 -6x<9,∴只需a≥9.∴a≥9.
在(-1,1)上恒成立,得a≥3x2-6x对x∈(-1,1)恒成立. ∵-1<x<1,∴3x2 -6x<9,∴只需a≥9.∴a≥9.

 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:不详 题型:解答题
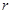 (米),试建立塑胶跑道面积S与
(米),试建立塑胶跑道面积S与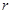 的函数关系S(
的函数关系S(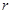 ) ,并求其定义域;
) ,并求其定义域; 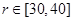 ,问当
,问当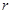 取何值时,运动场造价最低?(
取何值时,运动场造价最低?(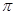 取3.14)
取3.14)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com