
 an-1+2n•3n-2(n≥2,n∈N?).
an-1+2n•3n-2(n≥2,n∈N?).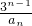 (n∈N?),数列{bn}的前n项和为Sn,试比较S2与n的大小;
(n∈N?),数列{bn}的前n项和为Sn,试比较S2与n的大小;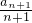 (n∈N*),数列{
(n∈N*),数列{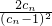 }的前n项和为Tn.求证:对任意n∈N*,都有 Tn<2.
}的前n项和为Tn.求证:对任意n∈N*,都有 Tn<2. 知,
知,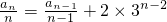 ,
,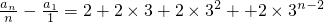
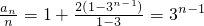
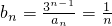 .
.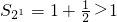 ;当n=2时,
;当n=2时,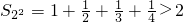 ;
; .
.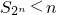 .
.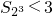 成立;
成立;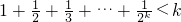 .
.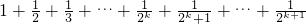
 ,
,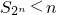 .
. ;当n=2时,
;当n=2时,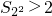 ;
;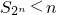 .
.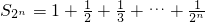
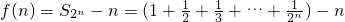
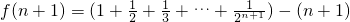

 ,此时
,此时 ;
; ,此时
,此时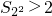 ;
;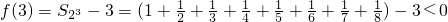 ,此时
,此时 ;
;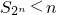 .
. ;当n≥3(n∈N*)时,
;当n≥3(n∈N*)时,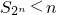 .
.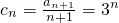
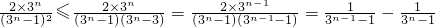
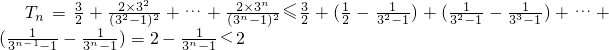 .
. 故对n∈N*,Tn<2得证.
故对n∈N*,Tn<2得证. ,从而可求出an.
,从而可求出an. 进行比较,从而猜想出一个结论,然后对这个结论用数学归纳法进行证明;
进行比较,从而猜想出一个结论,然后对这个结论用数学归纳法进行证明; 的差构造
的差构造 ,然后利用f(n+1)-f(n)的结果正负判断出f(n)的单调性.再通过n=1,2,3时,
,然后利用f(n+1)-f(n)的结果正负判断出f(n)的单调性.再通过n=1,2,3时,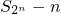 的结果变化趋势得出最后的结论.第3问先由an写出cn,然后先对
的结果变化趋势得出最后的结论.第3问先由an写出cn,然后先对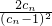 的用放缩法进行适当的放大,然后采用裂项法得出一个结果,然后再对Tn的除第一项以外的每一项按此进行放缩和裂项,运算之后很容易就看出与2的大小关系,就可以得出最后的证明结论.
的用放缩法进行适当的放大,然后采用裂项法得出一个结果,然后再对Tn的除第一项以外的每一项按此进行放缩和裂项,运算之后很容易就看出与2的大小关系,就可以得出最后的证明结论.

科目:高中数学 来源: 题型:
| n+1 |
| 2 |
| 2n |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com