
����Ŀ��ij��ѧ����רҵ400��ѧ���μ�ij�β�����������Ůѧ������������ʹ�÷ֲ�����ķ������������ȡ��100��ѧ������¼���ǵķ����������ݷֳ�7�飺[20,30����[30,40��������[80,90]���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
���������400��ѧ���������ȡһ�ˣ����������С��70�ĸ��ʣ�
������֪�����з���С��40��ѧ����5�ˣ��Թ��������з���������[40,50���ڵ�������
��������֪��������һ�������ķ�����С��70���������з�����С��70����Ů��������ȣ��Թ���������������Ů�������ı�����

���𰸡���1��0.4��2��20��3��3:2
���������������������������Ƶ��=������ߣ��ɵ÷���С��70�ĸ���Ϊ��1����0.04+0.02����10���������ȼ��������з���С��40��Ƶ�ʣ������������������[40��50���ڵ�Ƶ�ʣ��ɹ��������з���������[40��50���ڵ�������
��������֪��������һ�������ķ�����С��70���������з�����С��70����Ů��������ȣ������õ��𰸣�
���������
(1)��Ƶ�ʷֲ�ֱ��ͼ֪��
������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ��
��
������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ��
��
�����С��70��Ƶ��Ϊ![]() ��
��
�ʴ������400��ѧ���������ȡһ�ˣ����������С��70�ĸ���Ϊ![]() .
.
(2)��Ƶ�ʷֲ�ֱ��ͼ֪��
�����з���������![]() ������Ϊ
������Ϊ![]() (��)��
(��)��
��֪�����з���С��40��ѧ����5�ˣ�
���������з���������![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() (��)��
(��)��
�������з���������![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
��
��![]() ����
����![]() ��
��
���������з���������![]() �ڵ�����Ϊ20��.
�ڵ�����Ϊ20��.
(3)��Ƶ�ʷֲ�ֱ��ͼ֪��
������С��70������Ϊ![]() (��)��
(��)��
��֪������С��70����Ů��������ȣ�
�ʷ�����С��70�ֵ���������Ϊ30�ˣ�
����Ϊ��������һ�������ķ�����С��70��
��������Ƶ��Ϊ�� ![]() ��
��
��Ů����Ƶ��Ϊ�� ![]() ��
��
��������������Ů�������ı���ԼΪ�� ![]() .
.


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�IJ���ʽax2+��1��a��x��1��0
��1����a=2ʱ����ʽ�Ľ⼯��
��2����a����1ʱ����ʽ�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD���ⳤΪ2����AD��ƽ������ɵĽǦȡ�[ ![]() ��
�� ![]() ]���Ҷ���A��ƽ����ڣ�B��C��D����ƽ����⣬����BC���е�E��ƽ����ľ����ȡֵ��Χ�ǣ� ��
]���Ҷ���A��ƽ����ڣ�B��C��D����ƽ����⣬����BC���е�E��ƽ����ľ����ȡֵ��Χ�ǣ� �� 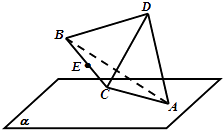
A.[ ![]() ��1]
��1]
B.[ ![]() ��1]
��1]
C.[ ![]() ��
�� ![]() ]
]
D.[ ![]() ��
�� ![]() ]
]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() Ϊ���Σ��ı���
Ϊ���Σ��ı���![]() Ϊƽ���ı��Σ���
Ϊƽ���ı��Σ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��

��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1��������![]() ��ֱ��
��ֱ��![]() ��ֱ�����߷��̣�
��ֱ�����߷��̣�
��2����![]() �ĵ����ݼ�������
�ĵ����ݼ�������
��3��������![]() ��ʹ����
��ʹ����![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڲ�������ˮ��Ⱦ���أ�Ϊ�˻�õ�һ�ֵ�ˮ�����ϣ�DZˮԱ��ҪDZ��ˮ��Ϊ60��ˮ������ҵ�����ݾ��飬DZˮԱ��DZ��ƽ���ٶ�Ϊ![]() ����/��λʱ�䣩��ÿ��λʱ����������
����/��λʱ�䣩��ÿ��λʱ����������![]() ����������ˮ����ҵ10����λʱ�䣬ÿ��λʱ����������
����������ˮ����ҵ10����λʱ�䣬ÿ��λʱ����������![]() ������������ˮ���ƽ���ٶ�Ϊ
������������ˮ���ƽ���ٶ�Ϊ![]() ����/��λʱ�䣩��ÿ��λʱ����������
����/��λʱ�䣩��ÿ��λʱ����������![]() ���������Ǹ�DZˮԱ��ɴ˴������������������Ϊ
���������Ǹ�DZˮԱ��ɴ˴������������������Ϊ![]() ������.
������.
��1����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����![]() ������DZ�ٶ�
������DZ�ٶ�![]() ȡʲôֵʱ��������������������.
ȡʲôֵʱ��������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �����溯����
�����溯����
��1����![]() ��
��
��2����![]() ������ʽ
������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��������
��������![]() �ķ���
�ķ���![]() ��Ψһʵ���⣬��ʵ��
��Ψһʵ���⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������![]() ��
��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ����
����![]() ��
��![]() �۵�
�۵�![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() .
.

������֤�� ![]() ƽ��
ƽ��![]() ��
��
������ƽ��![]() ��ƽ��
��ƽ��![]() �����е������ǵĴ�С.
�����е������ǵĴ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�е�ǰn���ΪSn= ![]() ����an=log2bn ��
����an=log2bn ��
��1��������{an}��ͨ�ʽ��
��2��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com