
分析 (1)先由条件利用互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式求得三次全都击中目标的概率,再用1减去此概率,即得所求.
(2)分别求出“甲射击2次,恰有2次击中目标”的概率、“乙射击2次,恰有1次击中目标”的概率,再把这两个概率相乘,即得所求.
解答 解:(1)记“甲连续射击3次至少有1次未击中目标”为事件A1,
由题意,射击3次,相当于3次独立重复试验,故 $P({A_1})=1-P(\overline{A_1})=1-{(\frac{2}{3})^3}=\frac{19}{27}$.
(2)记“甲射击2次,恰有2次击中目标”为事件A2,
“乙射击2次,恰有1次击中目标”为事件B2,则$P({A_2})=C_2^2×{(\frac{2}{3})^2}=\frac{4}{9}$,$P({B_2})=C_2^1×{(\frac{3}{4})^1}×(1-\frac{3}{4})=\frac{3}{8}$.
由于甲、乙射击相互独立,故 $P({A_2}{B_2})=\frac{4}{9}×\frac{3}{8}=\frac{1}{6}$.
点评 本题考查相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式,解答本题关键是判断出所研究的事件是那一种概率模型,属于基础题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [0.00,0.04] | 4 | 0.2 |
| (0.04,0.08] | 10 | 0.5 |
| (0.08,0.12] | 4 | 0.2 |
| (0.12,0.16] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 劳动生产率为1000元时,工资为130元 | |
| B. | 劳动生产率提高1000元,则工资提高80元 | |
| C. | 劳动生产率提高1000元,则工资提高130元 | |
| D. | 当月工资为210元时,劳动生产率为2000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=-\frac{π}{2}$ | B. | $x=-\frac{π}{4}$ | C. | $x=-\frac{π}{8}$ | D. | $x=\frac{5}{4}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{15}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
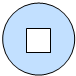 欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).
欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 命中环数 | 10 | 9 | 8 | 7 |
| 概 率 | 0.12 | 0.18 | 0.28 | 0.32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com