
(1)若P是A![]() ;
;
(2)求二面角A-A1B-C的大小.
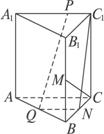
(1)解法一:取BC的中点N,连结QN、C1N.

∵AC⊥BC,AC⊥C
∴AC⊥平面B1BCC1.
又∵Q、N分别是AB、CB的中点,
∴QN∥AC.
∴QN⊥平面B1BCC1.
∴平面PQNC1⊥平面B1BCC1.
∴C1N是PQ在平面B1BCC1上的射影.
∵|C
∴PQ⊥CM.
∴![]() =0.
=0.
解法二:建立如图空间直角坐标系,则
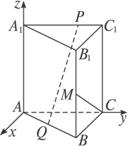
A(0,0,0),A1(0,0,1),C(0,![]() ,0),B(1,
,0),B(1, ![]() ,0),C1(0,
,0),C1(0,![]() ,1),M(1,
,1),M(1,![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ,0).
,0).
设P点坐标为(0,x,1),
∴![]() =(
=(![]() ,
,![]() -x,-1),
-x,-1), ![]() =(1,0,
=(1,0, ![]() ),
),
则![]() ·
·![]() =1×
=1×![]() +(-1)×
+(-1)×![]() =0,
=0,
即![]() ·
·![]() =0.
=0.
(2)解:作CH⊥AB于H,
∵A
∴CH⊥A

作HD⊥A1B于D,连结CD,
由三垂线定理得CD⊥A1B.
∴∠CDH为二面角A-A1B-C的平面角.
在Rt△ACB中,CH=![]() =
=![]() .
.
又∵A
又BC⊥AC,∴BC⊥平面A
易求得A1B=2,A![]() ,
,
∴在Rt△A1CB中,CD=![]() .
.
又在Rt△CHD中,sin∠CDH=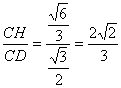 ,
,
故二面角A-A1B-C的大小为arcsin![]() .
.


科目:高中数学 来源:黄冈中学 高二数学(下册)、考试卷12 期末测试卷(B) 题型:044
如图所示,直三棱柱![]() 中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,
中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,![]() ,D为
,D为![]() 的中点,E为
的中点,E为![]() 的中点.
的中点.

(1)求直线BE与![]() 所成角的余弦值;
所成角的余弦值;
(2)试在线段![]() 上找到一点F,使CF⊥平面
上找到一点F,使CF⊥平面![]() ,并求出该点的坐标.
,并求出该点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
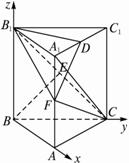
(1)求直线BE与A1C所成的角的余弦值.
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出|AF|;若不存在,请说明?理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
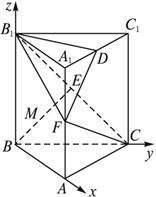
(1)求直线BE与A1C所成的角的余弦值.
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
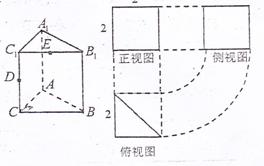
如图所示是直三棱柱A1B1C1-ABC的三视图, D、E分别是棱CC1和棱B1C1的中点,则在同一视角下,三棱锥E-ABD的三视图中,其侧视图的面积为( )
A.2 B.![]() C.3 D.4
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com