
【题目】已知F1 , F2是椭圆和双曲线的公共焦点,P是它们的一个公共点.且∠F1PF2= ![]() ,则椭圆和双曲线的离心率的倒数之和的最大值为( )
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
A.![]()
B.![]()
C.3
D.2
【答案】A
【解析】解:设椭圆的长半轴为a,双曲线的实半轴为a1 , (a>a1),半焦距为c, 由椭圆和双曲线的定义可知,
设|PF1|=r1 , |PF2|=r2 , |F1F2|=2c,
椭圆和双曲线的离心率分别为e1 , e2
∵∠F1PF2= ![]() ,
,
∴由余弦定理可得4c2=(r1)2+(r2)2﹣2r1r2cos ![]() ,①
,①
在椭圆中,①化简为即4c2=4a2﹣3r1r2 ,
即 ![]() ,②
,②
在双曲线中,①化简为即4c2=4a12+r1r2 ,
即 ![]() ,③
,③
联立②③得, ![]() =4,
=4,
由柯西不等式得(1+ ![]() )(
)( ![]() )≥(1×
)≥(1× ![]() +
+ ![]() )2 ,
)2 ,
即( ![]() )
) ![]() =
= ![]()
即 ![]()
![]() ,d当且仅当
,d当且仅当 ![]() 时取等号,
时取等号,
法2:设椭圆的长半轴为a1 , 双曲线的实半轴为a2 , (a1>a2),半焦距为c,
由椭圆和双曲线的定义可知,
设|PF1|=r1 , |PF2|=r2 , |F1F2|=2c,
椭圆和双曲线的离心率分别为e1 , e2
∵∠F1PF2= ![]() ,
,
∴由余弦定理可得4c2=(r1)2+(r2)2﹣2r1r2cos ![]() =(r1)2+(r2)2﹣r1r2 ,
=(r1)2+(r2)2﹣r1r2 ,
由 ![]() ,得
,得 ![]() ,
,
∴ ![]() =
= ![]() ,
,
令m=  =
= 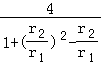 =
=  ,
,
当 ![]() 时,m
时,m ![]() ,
,
∴ ![]() ,
,
即 ![]() 的最大值为
的最大值为 ![]() ,
,
法3:设PF1|=m,|PF2|=n,则 ![]() ,
,
则a1+a2=m,
则 ![]() =
= ![]() ,
,
由正弦定理得 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() sin(120°﹣θ)≤
sin(120°﹣θ)≤ ![]() =
= ![]()
故选:A
根据双曲线和椭圆的性质和关系,结合余弦定理即可得到结论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2
B.6
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,求: 
(1)直线PQ与CD所成角的大小
(2)四面体PCDQ的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,则实数a的取值范围是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线c1:y2=2px(p>0)与曲线c2:(x﹣6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且 ![]() =0.
=0. 
(1)求曲线c1的方程;
(2)过定点M(3,2)的直线l与曲线c1交于A,B两点,若点M是线段AB的中点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= ![]() .
.
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦;
(Ⅲ)求点E到平面ACD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:①f(0)=0,②f(x)+f(1﹣x)=1,③f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )+f(
)+f( ![]() )等于( )
)等于( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com