Question

（06年湖北卷理）（12分）

如图，在棱长为1的正方体中，是侧棱上的一点，。

（Ⅰ）、试确定，使直线与平面所成角的正切值为；

（Ⅱ）、在线段上是否存在一个定点Q，使得对任意的，D₁Q在平面上的射影垂直于，并证明你的结论。

Answer 1

点评：本小题主要考查线面关系、直线于平面所成的角的有关知识及空间想象能力和推理运算能力，考查运用向量知识解决数学问题的能力。

解析：解法1：（Ⅰ）连AC，设AC与BD相交于点O,AP与平面相交于点，,连结OG，

因为PC∥平面，平面∩平面APC＝OG,

故OG∥PC，所以，OG＝PC＝.

又AO⊥BD,AO⊥BB1，所以AO⊥平面，

故∠AGO是AP与平面所成的角.

在Rt△AOG中，tanAGO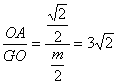＝，即m＝.

所以，当m＝时，直线AP与平面所成的角的正切值为.

（Ⅱ）可以推测，点Q应当是A_IC_I的中点O₁，因为

D₁O₁⊥A₁C₁, 且 D₁O₁⊥A₁A ，所以 D₁O₁⊥平面ACC₁A₁，

又AP平面ACC₁A₁，故 D₁O₁⊥AP.

那么根据三垂线定理知，D₁O₁在平面APD₁的射影与AP垂直。