练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    定义在R上的奇函数f（x）在（0，+∞）上单调递减，且f（1）=0，则不等式xf（x）≥0的解集为________．

    [0，1]∪（-∞，-1]
    分析：先确定函数f（x）在（-∞，0）上单调递减，且f（-1）=0，再将不等式等价变形，即可得到结论．
    解答：∵定义在R上的奇函数f（x）在（0，+∞）上单调递减，且f（1）=0，
    ∴函数f（x）在（-∞，0）上单调递减，且f（-1）=0，
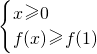
    ∴不等式xf（x）≥0等价于或
    ∴0≤x≤1或x≤-1
    ∴不等式xf（x）≥0的解集为[0，1]∪（-∞，-1]
    故答案为：[0，1]∪（-∞，-1]
    点评：本题考查函数单调性与奇偶性的结合，考查学生的计算能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    定义在R上的奇函数f（x）满足f（2x）=-2f（x），f(-1)=
    1
    2
    ，则f（2）的值为（　　）
    A、-1B、-2C、2D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的奇函数f（x）在（0，+∞）上是增函数，又f（-3）=0，则不等式xf（x）＜0的解集为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的奇函数f（x）在[0，+∞）是增函数，判断f（x）在（-∞，0）上的增减性，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的奇函数f（x）满足：当x＞0时，f（x）=2010x+log2010x，则方程f（x）=0的实根的个数为
    3
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在R上的奇函数f（x），当x≥0时，f（x）=x3+x2，则f（x）=
    x3+x2    x≥0
     
    x3-x2     x＜0
    x3+x2    x≥0
     
    x3-x2     x＜0
    ．

    查看答案和解析>>

    同步练习册答案