
【题目】若an=log(n+1)(n+2)(n∈N),我们把使乘积a1a2…an为整数的数n叫做“劣数”,则在区间(1,2004)内所有劣数的和为 .
【答案】2026
【解析】解:∵an=log(n+1)(n+2) ∴a1=log23;a2=log34;a3=log45;…
则a1a2…an=log23log34log45…log(n+1)(n+2)=log2(n+2)
当n+2为2的整数次幂时,a1a2…an为整数
则在区间(1,2004)内所有劣数n,对应的n+2构成一个以4为首项,以2为公比的等比数列,且满足条件的最后一项为1024
则区间(1,2004)内所有劣数的和为:
(4﹣2)+(8﹣2)+(16﹣2)+…+(1024﹣2)=(4+8+16+…+1024)﹣2×9=2044﹣18=2026
所以答案是:2026
【考点精析】解答此题的关键在于理解对数的运算性质的相关知识,掌握①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos2α+cos2β=1类比到空间,在长方体中,一条对角线与从其一顶点出发的三个面所成的角分别为α,β,γ,则有cos2α+cos2β+cos2γ= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2﹣ax,g(x)=lnx,h(x)=f(x)+g(x)
(1)若f(x)≥g(x)对于公共定义域内的任意x恒成立,求实数a的取值范围;
(2)设h(x)有两个极值点x1 , x2 , 且x1∈(0, ![]() ),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1 , 下列判断中一定正确的是( ) 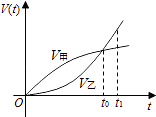
A.在t1时刻,甲车在乙车前面
B.t1时刻后,甲车在乙车后面
C.在t0时刻,两车的位置相同
D.t0时刻后,乙车在甲车前面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,分别求函数
时,分别求函数![]() 的最小值和
的最小值和![]() 的最大值,并证明当
的最大值,并证明当![]() 时,
时, ![]() 成立;
成立;
(3)令![]() ,当
,当![]() 时,判断函数
时,判断函数![]() 有几个不同的零点并证明.
有几个不同的零点并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com