
【题目】已知关于![]() 的不等式
的不等式![]() .
.
(1)当![]() 时,解不等式;
时,解不等式;
(2)如果不等式的解集为空集,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)当![]() 时,不等式
时,不等式![]() 变为
变为![]() 。由绝对值的意义,按绝对值号内的
。由绝对值的意义,按绝对值号内的![]() 的正负,分三种情况讨论:当
的正负,分三种情况讨论:当![]() 时,不等式变为
时,不等式变为![]() ;当
;当![]() 时,不等式变为
时,不等式变为![]() ,恒成立,所以
,恒成立,所以![]() 符合不等式;当
符合不等式;当![]() 时,不等式变为
时,不等式变为![]() 。取三种情况的并集,可得原不等式的解集。(2)解法一:构造函数
。取三种情况的并集,可得原不等式的解集。(2)解法一:构造函数![]() 与
与![]() ,原不等式的解集为空集,
,原不等式的解集为空集, ![]() 的最小值比大于或等于
的最小值比大于或等于![]() ,作出
,作出![]() 与
与![]() 的图象. 只须
的图象. 只须![]() 的图象在
的图象在![]() 的图象的上方,或
的图象的上方,或![]() 与
与![]() 重合,
重合, ![]() 。解法二:构造函数
。解法二:构造函数![]() ,讨论绝对值号内式子得正负去掉绝对值可得,
,讨论绝对值号内式子得正负去掉绝对值可得, ![]()
 ,求每一段函数的值域,可得函数的最小值
,求每一段函数的值域,可得函数的最小值![]() =1,
=1, ![]() 小于等于函数的最小值1.解法三,由不等式
小于等于函数的最小值1.解法三,由不等式![]() 可得
可得![]() ,当且仅当
,当且仅当![]() 时,上式取等号,∴
时,上式取等号,∴![]() .
.
试题解析:解:(1)原不等式变为![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() ,∴
,∴ ![]()
当![]() 时,原不等式化为
时,原不等式化为![]() ,∴
,∴ ![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() ,∴
,∴ ![]() .
.
综上,原不等式解集为![]() .
.
(2)解法一:作出![]() 与
与![]() 的图象.
的图象.
若使![]() 解集为空集,
解集为空集,
只须![]() 的图象在
的图象在![]() 的图象的上方,或
的图象的上方,或![]() 与
与![]() 重合,
重合,
∴![]() ,所以
,所以![]() 的范围为
的范围为![]() .
.

解法二: ![]()
 ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
综上![]() ,原问题等价于
,原问题等价于![]() ,∴
,∴ ![]() .
.
解法三:∵![]() ,当且仅当
,当且仅当![]() 时,上式取等号,∴
时,上式取等号,∴![]() .
.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R). 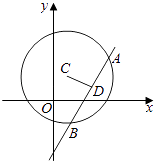
(1)求证:无论m取什么实数,直线l恒过第一象限;
(2)求直线l被圆C截得的弦长最短时m的值以及最短长度;
(3)设直线l与圆C相交于A、B两点,求AB中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为(1,1)的圆C经过点M(1,2).
(1)求圆C的方程;
(2)若直线x+y+m=0与圆C交于A、B两点,且△ABC是直角三角形,求实数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣4ax+b(a>0)在区间[0,1]上有最大值1和最小值﹣2.
(1)求a,b的值;
(2)若不等式f(x)≥mx在x∈(0,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域R上的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.
,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα﹣
=(cosα﹣ ![]() ,﹣1),
,﹣1), ![]() =(sinα,1),
=(sinα,1), ![]() 与
与 ![]() 为共线向量,且α∈[﹣
为共线向量,且α∈[﹣ ![]() ,0].
,0].
(1)求sinα+cosα的值;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若an=log(n+1)(n+2)(n∈N),我们把使乘积a1a2…an为整数的数n叫做“劣数”,则在区间(1,2004)内所有劣数的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.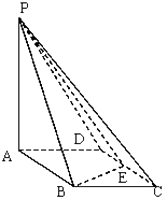
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com