
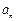 逐月递增且控制在2万件内;
逐月递增且控制在2万件内;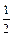 an2 (n∈N*)
an2 (n∈N*)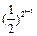
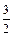 ①
①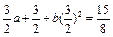 ②
②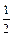 从而an + 1 =" 2an" –
从而an + 1 =" 2an" –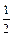 an2 (n∈N*) ………………………5分
an2 (n∈N*) ………………………5分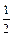 an2 = –
an2 = –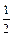 (an – 2)2 + 2≤2.
(an – 2)2 + 2≤2.  <2
<2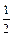 an2 + 2an – an = –
an2 + 2an – an = –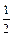 an (an – 2) >0,
an (an – 2) >0,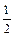 x2 + 2x = –
x2 + 2x = –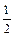 (x – 2)2 + 2在[0,2]上为增函数,
(x – 2)2 + 2在[0,2]上为增函数,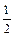 ak (4 – ak) <
ak (4 – ak) <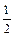 ak + 1(4 –ak + 1) <
ak + 1(4 –ak + 1) <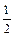 ×2×(4 – 2)
×2×(4 – 2) 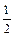 an2得2 (an + 1– 2) =" –" (an – 2)2 即(2 – an + 1) =
an2得2 (an + 1– 2) =" –" (an – 2)2 即(2 – an + 1) = 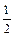 (2 – an)2
(2 – an)2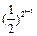 (n∈N*)为所求………13分
(n∈N*)为所求………13分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
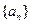 的通项公式为
的通项公式为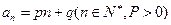 . 数列
. 数列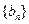 定义如下:对于正整数m,
定义如下:对于正整数m,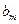 是使得不等式
是使得不等式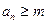 成立的所有n中的最小值.
成立的所有n中的最小值.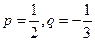 ,求
,求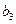 ;
;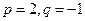 ,求数列
,求数列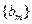 的前2m项和公式;
的前2m项和公式;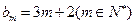 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
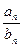 }的前n项和Sn;
}的前n项和Sn;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com