练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=f（x）是定义在（-∞，+∞）上的奇函数．若x＞0时、f（x）=log 
    1
    2
    x，则f（-2）+f（0）=
     
    ．
    考点：函数奇偶性的性质,对数的运算性质
    专题：函数的性质及应用
    分析：由题意可得f（0）=0，f（-2）=-f（2）=1，相加可得答案．
    解答： 解：∵函数y=f（x）是定义在（-∞，+∞）上的奇函数，∴f（0）=0，
    又∵x＞0时、f（x）=log 
    1
    2
    x，∴f（-2）=-f（2）=1，
    ∴f（-2）+f（0）=1，
    故答案为：1．
    点评：本题考查函数的奇偶性，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}的前n项和为Sn，且Sn=2an-2，则a2等于（　　）
    A、4B、2C、1D、-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过双曲线
    x2
    a2
    -
    y2
    b2
    =1，（a＞0，b＞0）的右焦点F作垂直于x轴的直线，交双曲线的渐近线于A、B两点，若△OAB（O为坐标原点）是等边三角形，则双曲线的离心率为（　　）
    A、
    		3
    3
    B、
    2
    		3
    3
    C、
    		3
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某射击运动员在一次测试中射击10次，其测试成绩如下表：
    环数78910
    频数3223
    则该运动员初试成绩的中位数为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数y=cos2x+asinx-
    1
    2
    a-
    3
    2
    的最大值是1，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）=2cos2x+
    		3
    sin2x+a（a∈R，a为常数）
    （1）若x∈R，求函数f（x）单调增区间；
    （2）若f（x）在[-
    π
    6
    ，
    π
    6
    ]上的最大值与最小值之和为3，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

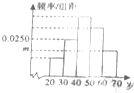    为了“城市品位、方便出行、促进发展”，近年合肥市正在修建地铁1号线，市某部门问卷调查了n个市民，其中赞城修建地铁的市民占80%，在赞城修建地铁的市民中又按年龄分组，得样本频率分布直方图如图，其中年龄在[30，40]岁的有2500人，年龄在[60，70）岁的有2000人，则m，n的值分别为（　　）
    A、0.2，12500
    B、0.2，10000
    C、0.02，12500
    D、0.02，10000

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法错误的是（　　）
    A、两两相交且不过同一点的三条直线必在同一平面内
    B、过直线外一点有且只有一个平面与已知直线垂直
    C、如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直
    D、如果两条直线和一个平面所成的角相等，则这两条直线一定平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中是假命题的是（　　）
    A、?a，b∈R*，lg（a+b）≠lga+lgb
    B、?φ∈R，使得函数f（x）=sin（2x+φ）是偶函数
    C、?α，β∈R，使得cos（α+β）=cosα+cosβ
    D、?m∈R，使f（x）=（m-1）•x m2-2m+3是幂函数，且在（0，+∞）上递减

    查看答案和解析>>

    同步练习册答案