
已知圆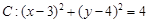 ,
,
(Ⅰ)若直线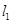 过定点
过定点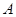 (1,0),且与圆
(1,0),且与圆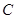 相切,求
相切,求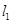 的方程;
的方程;
(Ⅱ) 若圆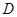 的半径为3,圆心在直线
的半径为3,圆心在直线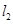 :
: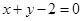 上,且与圆
上,且与圆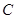 外切,求圆
外切,求圆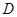 的方程.
的方程.
(Ⅰ) 或
或 ; (Ⅱ)
; (Ⅱ) 
【解析】
试题分析:(Ⅰ)此问注意直线斜率不存在的情况,应分斜率是否存在进行讨论,当斜率存在时由圆心到直线的距离等于半径求出直线斜率; (Ⅱ)先设出圆心坐标,然后由两圆外切,知圆心距等于两半径之和,从而求出圆心D的坐标,写出圆D方程.
试题解析:(Ⅰ)①若直线 的斜率不存在,即直线是
的斜率不存在,即直线是 ,符合题意.
,符合题意.
②若直线 斜率存在,设直线
斜率存在,设直线 为
为 ,即
,即 .
.
由题意知,圆心(3,4)到已知直线 的距离等于半径2,
的距离等于半径2,
即  解之得
解之得  .所求直线方程是
.所求直线方程是 ,
, .
.
(Ⅱ)依题意设 ,又已知圆的圆心
,又已知圆的圆心 ,
,
由两圆外切,可知
∴可知  =
= ,
解得
,
解得  ,
∴
,
∴ 
 ,
,
∴ 所求圆的方程为  .
.
考点:1.直线与圆相切;2.两圆相外切;3.点到直线的距离公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(09年莱西一中模拟)(12分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为![]() m,圆环的圆心距离地面的高度为
m,圆环的圆心距离地面的高度为![]() ,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度![]() ;
;
(2)画出函数![]() 在
在![]() 时的图象;
时的图象;
(3)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过![]() m?
m?

查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省皖南八校高三第一次联考理科数学试卷 题型:解答题
(本小题满分12分)已知椭圆 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直
线倾斜角为 ,原点到该直线的距离为
,原点到该直线的距离为 .
.
(1)求椭圆的方程;
(2)斜率小于零的直线过点D(1,0)与椭圆交于M,N两点,若 求直线MN的方程;
求直线MN的方程;
(3)是否存在实数k,使直线 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:河北省高三下学期第二次考试数学(文) 题型:解答题
(本题满分12分)已知椭圆 的离心率为
的离心率为 ,
,
直线 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左焦点为F1,右焦点为F2,直线
的左焦点为F1,右焦点为F2,直线 过点F1,且垂直于椭圆的长轴,动直
过点F1,且垂直于椭圆的长轴,动直
线 垂直
垂直 于点P,线段PF2的垂直平分线交
于点P,线段PF2的垂直平分线交 于点M,求点M的轨迹C2的方程;
于点M,求点M的轨迹C2的方程;
(Ⅲ)若AC、BD为椭圆C1的两条相互垂直的弦,垂足为右焦点F2,求四边形ABCD的面积
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
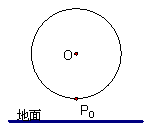 (8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为
(8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为![]() m,圆环的圆心距离地面的高度为
m,圆环的圆心距离地面的高度为![]() ,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度![]() ;
;
(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过![]() m?
m?
查看答案和解析>>
科目:高中数学 来源: 题型:
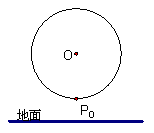 (8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为
(8分)如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为![]() m,圆环的圆心距离地面的高度为
m,圆环的圆心距离地面的高度为![]() ,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
,蚂蚁每分钟爬行一圈,若蚂蚁的起始位置在最低点P0处.
(1)试确定在时刻t时蚂蚁距离地面的高度![]() ;
;
(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过![]() m?
m?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com