
解析:设椭圆方程为![]() =1(a>b>0),直线l与y轴相交于A点,连结F1A.
=1(a>b>0),直线l与y轴相交于A点,连结F1A.
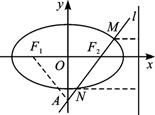
由已知可得△F1AF2为等腰直角三角形,且|F1A|=![]() ,
,
∴|F1F2|=2.∴c=1,F2(1,0).
∴直线l的方程为y=x-1.
设M(x1,y1)、N(x2,y2),由已知
(![]() -x1)+(
-x1)+(![]() -x2)=
-x2)=![]()
![]() x1+x2=
x1+x2=![]() -
-![]() =2a2-
=2a2-![]() .
.
从而y1+y2=(x1-1)+(x2-1)=x1+x2-2=2a2-![]() .
.
∵M、N在椭圆上,∴![]() =1,
=1,![]() =1,两式相减,得
=1,两式相减,得![]() =0
=0 ![]() b2(x1+x2)+a2(y1+y2)·
b2(x1+x2)+a2(y1+y2)·![]() =0.
=0.
∴b2(2a2-![]() )+a2(2a2-
)+a2(2a2-![]() )=0,
)=0,
即(a2-1)(2a2-![]() )+a2(2a2-
)+a2(2a2-![]() )=0.
)=0.
∴a2=![]() 或a2=2(a2=
或a2=2(a2=![]() 舍去).
舍去).
∴b2=a2-1=1.∴椭圆方程为![]() =1.
=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

(1)求飞船飞行的椭圆轨道的方程;
(2)飞船绕地球飞行了十四圈后,于16日5时59分返回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105 km,问飞船巡天飞行的平均速度是多少?(结果精确到1 km/s)(注:km/s即千米/秒)
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求飞船飞行的椭圆轨道的方程;
(2)飞船绕地球飞行了十四圈后,于16日5时59分返回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105 km,问飞船巡天飞行的平均速度是多少?(结果精确到1 km/s)(注:km/s即千米/秒)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
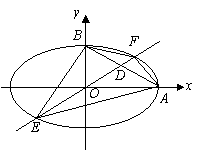
(如图)设椭圆中心在坐标原点,![]() 是它的两个顶点,直线
是它的两个顶点,直线
![]() 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
 (1)若
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com