
设
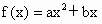 ,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
|
解法 1:1≤f(-1)=a-b≤2,2≤f(1)=a+b≤4.两式相加,得 3≤2a≤6,∴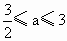 . .
又∵- 2≤b-a≤-1,2≤b+a≤4,∴ 0≤2b≤3.∴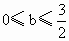 . .
∴ 6≤4a≤12,-3≤-2b≤0.∴ 3≤f(-2)=4a-2b≤12.解法 2:由f(-1)=a-b,f(1)=a+b,得 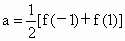 , ,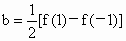 . .
∴ f(-2)=4a-2b=f(1)+3f(-1).∵ 1≤f(-1)≤2,∴3≤3f(-1)≤6.又 2≤f(1)≤4,∴5≤f(-2)≤10. |
|
比较上述两种解法,所得结果分别为 3≤f(-2)≤12与5≤f(-2)≤10.显然结果不同,为什么呢?考虑条件1≤f(-1)≤2,2≤f(1)≤4,得到的是1≤a-b≤2,2≤a+b≤4这两个结论,显然a、b两字母是相互联系的整体而并不独立存在着,如果确定出a、b的各自范围 , ,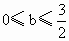 ,那么0≤a-b≤3, ,那么0≤a-b≤3, ,即0≤f(-1)≤3, ,即0≤f(-1)≤3, ,这与条件矛盾了!因此,解法1方法错了,本题的答案应该是5≤f(-2)≤10. ,这与条件矛盾了!因此,解法1方法错了,本题的答案应该是5≤f(-2)≤10.
总结本题,可知:如果条件是多个字母相关连 (如和、差、积、商等)的范围,在求解与这些字母有关代数式范围时,我们利用整体代换的方式,把要求范围的代数式用已知代数式表示,再利用不等式性质求解.这种整体思想要注意把握和运用.f( -1)=a-b,f(1)=a+b,一方面,由条件知1≤a-b≤2,2≤a+b≤4,因此可确定字母a、b的范围,进而求出f(-2)的范围;另一方面,由f(-1),f(1)可求出 |


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源:甘肃省西北师大附中2012届高三第一学期期中考试数学理科试题 题型:013
设函数y=f(x)存在反函数y=f-1(x),且函数y=x-f(x)的图象过点(1,2),则函数y=f-1(x)-x的图象一定过点
(1,2)
(2,0)
(-1,2)
(2,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com