
如图,△ABC中,AC=BC=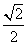 AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
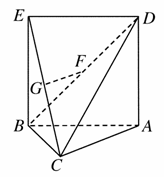
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.
[解] (1)证明:连接AE,如下图所示.
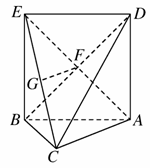
∵ADEB为正方形,
∴AE∩BD=F,且F是AE的中点,
又G是EC的中点,
∴GF∥AC,又AC⊂平面ABC,GF⊄平面ABC,
∴GF∥平面ABC.
(2)证明:∵ADEB为正方形,∴EB⊥AB,
又∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EB⊂平面ABED,
∴BE⊥平面ABC,∴BE⊥AC.
又∵AC=BC=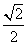 AB,
AB,
∴CA2+CB2=AB2,
∴AC⊥BC.
又∵BC∩BE=B,∴AC⊥平面BCE.
(3)取AB的中点H,连GH,∵BC=AC=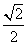 AB=
AB=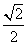 ,
,
∴CH⊥AB,且CH= ,又平面ABED⊥平面ABC
,又平面ABED⊥平面ABC
∴GH⊥平面ABCD,∴V=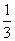 ×1×
×1× =
=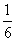 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知函数f(x)=4x+3sin x,x∈(-1,1),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A.(0,1) B.(1, )
)
C.(-2,- ) D.(-∞,-2)∪(1,+∞)
) D.(-∞,-2)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com